Select Question Set:
Q. No.An equiconvex lens of focal length \(100\) cm is split into two plano-convex lenses and the plane surface of one of these lenses is silvered. This acts as a:
1.
converging mirror of focal length \(200\) cm.
2.
converging mirror of focal length \(100\) cm.
3.
diverging mirror of focal length \(200\) cm.
4.
diverging mirror of focal length \(100\) cm.
Subtopic: Lenses |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Two identical equilateral triangular prisms, each of which gives a minimum deviation of \(60^{\circ}\) are taken: call these prisms \(A,B\). These are placed as shown in the figure, and a ray of light is incident on prism \(A\) at minimum deviation. Now prism \(B\) is cut in half, along the dotted line, and the right half is removed. The deviation of the emerging ray is:
| 1. | \(90^{\circ}\) | 2. | \(45^{\circ}\) |
| 3. | \(60^{\circ}\) | 4. | \(30^{\circ}\) |
Subtopic: Prisms |
51%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A thin plane parallel slab (thickness \(t\), refractive index \(\mu\)) is placed just behind a converging lens of focal length \(f.\) If a parallel beam of light is incident on the combination it will converge at a distance of:
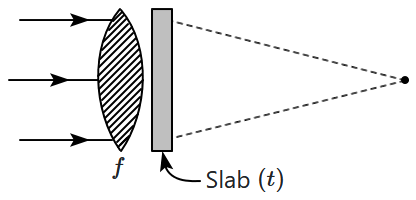
| 1. | \(f\) from the end of the slab. |
| 2. | \(f-\frac{t}{\mu}\) from the end of the slab. |
| 3. | \(f+\frac{t}{\mu}\) from the end of the slab. |
| 4. | \(f+t\Big(1-\frac{1}{\mu}\Big)\) from the end of the slab. |
Subtopic: Refraction at Curved Surface |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A convex lens of focal length \(60\) cm is placed in the path of a parallel beam, falling parallel to its principal axis. A plane mirror is placed on the principal axis, making an angle of \(45^{\circ}\) with it, at a distance of \(30\) cm behind the lens. The distance of the new focus from lens (optical centre) is:
1. \(60\) cm
2. \((60+30\sqrt2)\) cm
3. \(60\sqrt2\) cm
4. \(30\sqrt2\) cm
1. \(60\) cm
2. \((60+30\sqrt2)\) cm
3. \(60\sqrt2\) cm
4. \(30\sqrt2\) cm
Subtopic: Lenses |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A parallel beam of width \(20\) mm is incident onto a lens and the width of the emerging beam decreases at a rate of \(1\) mm as it travels every \(3\) cm. The lens has a focal length of:
| 1. | \(30\) cm | 2. | \(60\) cm |
| 3. | \(\dfrac{20}3\) cm | 4. | \(\dfrac{40}{3}\) cm |
Subtopic: Lenses |
63%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
An empty cylindrical beaker whose height is equal to its diameter is kept on a table. An observer's eye\((E)\) looking towards \(S\) (line of sight: \(ES\)) can see the point \(Q\) on the lower right. The angle of view, \(\theta,\) is the angle the line of sight \(ES,\) makes with the vertical \(RS\)-extended. A transparent liquid is now slowly poured into the beaker. As the liquid level rises in the beaker, the line of sight has to be continually adjusted (by increasing angle \(\theta\)) in order to keep \(Q\) visible. When the liquid fills the beaker to the brim, \(Q\) can no more be seen by adjusting the line of sight \(ES. \) The minimum refractive index of the liquid should be:
| 1. | \(\dfrac32\) | 2. | \(2\) |
| 3. | \(\sqrt{\dfrac32} \) | 4. | \(\sqrt2\) |
Subtopic: Total Internal Reflection |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Assume that the corner of \(O\) of the room is the origin, and the axes \(x,y,z\) are along the edges. The three walls meeting orthogonally at \(O\) are perfect mirrors. A ray of light travelling parallel to the vector \(-(\hat i+2\hat j+\hat k)\) is incident on the \(y\text-z\) mirror (wall). The emerging ray, after all reflections, will be along:
| 1. | \(\hat i-2\hat j-\hat k\) |
| 2. | \(\hat i+\hat k-2\hat j\) |
| 3. | \(-\hat i+2\hat j+\hat k\) |
| 4. | \(\hat i+2\hat j+\hat k\) |
Subtopic: Reflection at Plane Surface |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
An equilateral triangular prism of glass \((\mu=1.5)\) is placed in air. A ray of light is incident normally onto the surface \(AB.\) The ray will finally emerge:
| 1. | normally from the surface \(BC.\) |
| 2. | normally from the surface \(AC.\) |
| 3. | either from the surface \(BC\) or \(AC,\) normally. |
| 4. | either from the surface \(BC\) or \(AC,\) at an angle of emergence greater than \(60^{\circ}\) but less than \(90^{\circ}.\) |
Subtopic: Total Internal Reflection |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Given below are two statements:
| Assertion (A): | If two converging lenses are introduced into the path of a parallel beam of light, the emerging beam cannot be diverging. |
| Reason (R): | The converging lenses have positive powers. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | (A) is False but (R) is True. |
Subtopic: Lenses |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A parallel beam of light of intensity \(I_0\) is incident on a lens and the intensity of the emerging beam is \(4I_0\) after it has traversed a further distance of \(30\) cm from the lens. The focal length of the lens is:
1. \(40\) cm
2. \(20\) cm
3. \(45\) cm
4. \(60\) cm
1. \(40\) cm
2. \(20\) cm
3. \(45\) cm
4. \(60\) cm
Subtopic: Lenses |
52%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Select Question Set:
© 2025 GoodEd Technologies Pvt. Ltd.