A body of mass \(m\) is slipping on a rough horizontal plane, decelerating at \(6\) m/s2. The net force exerted by the plane on the body is: (take \(g =10~\text{m/s}^{2}\))
1. \(1.6~mg\)
2. \(0.4~mg\)
3. \(\sqrt{1.36}~mg\)
4. \(\sqrt{1.16}~mg\)
A block of mass \(1\) kg is suspended by means of a spring, and the system is at rest. An additional force is now applied to the block and it accelerates downward at '\(g\)' \((g =10~\text{m/s}^2)\). At this moment, the force exerted by the spring on the block will be:

| 1. | \(10~\text{N}\) | 2. | \(15~\text{N}\) |
| 3. | \(20~\text{N}\) | 4. | zero |
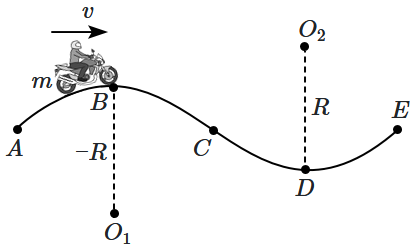
Then:
| 1. | \(N_{B}=m g+\dfrac{m v^{2}}{R}\) \(N_{D}=m g-\dfrac{m v^{2}}{R}\) |
2. | \(N_{B}=m g-\dfrac{m v^{2}}{R}\) \(N_{D}=m g+\dfrac{m v^{2}}{R}\) |
| 3. | \(N_{B}=m g+\dfrac{m v^{2}}{R}\) \(N_{D}=\dfrac{m v^{2}}{R}-m g\) |
4. | \(N_{B}=\dfrac{m v^{2}}{R}-m g\) \(N_{D}=\dfrac{m v^{2}}{R}+m g\) |
A block of mass \(m\) is placed on a smooth inclined surface of a wedge of mass \(M\). The system is placed on a smooth horizontal table and released.

| 1. | The acceleration of \(m\) is \(g\sin\theta\), and that of \(M\) is zero. |
| 2. | The acceleration of \(m\) is less than \(g\sin\theta\), and that of \(M\) is to the left. |
| 3. | The acceleration of \(m\) is greater than \(g\sin\theta\), and that of \(M\) is to the left. |
| 4. | Any of the above may be true depending on the values of \(m\) and \(M\). |
The two blocks \(A\) and \(B\) are placed on a smooth horizontal plane, with the string initially just taut. Forces are applied as shown. The tension in the string is:

| 1. | \(5~\text{N}\) | 2. | \(2~\text{N}\) |
| 3. | \(1~\text{N}\) | 4. | \(0~\text{N}\) |
The two blocks are at rest on a smooth horizontal plane and are connected by strings passing over a smooth light pulley as shown. The strings are vertical while the force \(F,\) applied to the pulley is vertical. For what minimum value of \(F\) will the \(2\) kg block be lifted off?
(\(g=10\) m/s2)
| 1. | \(20\) N | 2. | \(30\) N |
| 3. | \(25\) N | 4. | \(40\) N |
An elevator moving up is decelerating at \(1\) m/s2. Then, the apparent weight of a \(50\) kg man, on a weighing machine, will be: (take \(g=\) \(10\) m/s2)
| 1. | \(55\) kg | 2. | \(45\) kg |
| 3. | \(40\) kg | 4. | none of the above |
An astronaut, in a space shuttle, orbiting close to the earth's surface (take \(g= 10~\text{m/s}^2\)), suddenly fires his engines so as to give him a forward acceleration of \(\dfrac{3g}{4}\) along the direction of his motion. At that instant, his apparent weight is:
| 1. | \(25\%\) more than his real weight. |
| 2. | \(25\%\) less than his real weight. |
| 3. | \(75\%\) more than his real weight. |
| 4. | \(75\%\) less than his real weight. |
The mass \(m\) can slide along a smooth radial groove in a horizontal turntable; at the other end is attached a spring- so that the mass \(m\) presses against the spring as it moves 'outward'. The free-end (\(A\)) of the spring is at a distance \(b\) from the centre and the spring constant is \(k.\) If the turntable is rotated with an angular speed \(\omega\), and the mass \(m\) is in 'equilibrium' with the spring compressed, then the compression is:

| 1. | \(\dfrac{m\omega^2b}{k}\) |
| 2. | \(\dfrac{m\omega^2b}{k-m\omega^2}\) |
| 3. | \(\dfrac{m\omega^2b}{m\omega^2-k}\) |
| 4. | \(\dfrac{m\omega^2b}{m\omega^2+k}\) |
1. \(1000~\text{N}\)
2. \(2500~\text{N}\)
3. \(1500~\text{N}\)
4. \(3500~\text{N}\)








