Select Question Set:
Q. No.An AC-voltage is applied across the ends \(A,B\) of the circuit shown in the figure, the RMS voltage being \(V_0\). It is observed that the RMS currents in all the three branches are equal to \(\dfrac{V_0}{R}\). The total current entering at \(A\) equals:
| 1. | \(\dfrac{V_0}{R}\) | 2. | \(\sqrt{2}\dfrac{V_0}{R}\) |
| 3. | \(\Big(\sqrt{2}+1\Big)\dfrac{V_0}{R}\) | 4. | \(\sqrt{3}\dfrac{V_0}{R}\) |
Subtopic: Different Types of AC Circuits |
69%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The charge flowing through a resistance \(R\) is given by
\(q = A\sin\omega t+B\cos\omega t\)
The heat produced in the resistance over a very long time \(\Delta t\) (much greater than \(T = \dfrac{2\pi}{\omega}\)) is:
| 1. | \(\omega^{2}\left(A^{2}+B^{2}\right) R \Delta t\) |
| 2. | \(\omega^{2}\left(A^{2}-B^{2}\right) R \Delta t\) |
| 3. | \(\dfrac{1}{2} \omega^{2}\left(A^{2}+B^{2}\right) R \Delta t\) |
| 4. | \(\dfrac{1}{2} \omega^{2}\left(A^{2}-B^{2}\right) R \Delta t\) |
Subtopic: Power factor |
66%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
An inductor \(200\) mH, capacitor \(20~\mu\text{F}\) and a resistance of \(200~\Omega\) are connected in series across a source of emf, \(E = (20~\text{V})\sin(500t)\), where \(t\) is in second. The power loss in the circuit is:
1. \(2~\text{W}\)
2. \(1~\text{W}\)
3. \(0.5~\text{W}\)
4. \(0.25~\text{W}\)
Subtopic: Different Types of AC Circuits |
69%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
In an AC-circuit, the applied voltage is
\(e=V_0\sin(wt)\)
and the current, \(i\) is
\(i=I_0\cos(wt-\phi).\) The average power dissipated per cycle is:
\(e=V_0\sin(wt)\)
and the current, \(i\) is
\(i=I_0\cos(wt-\phi).\) The average power dissipated per cycle is:
| 1. | \(V_{0} I_{0} {\cos\phi}\) |
| 2. | \(\dfrac{V_{0} I_{0} \cos \phi}{2}\) |
| 3. | \(V_{0} I_{0} \sin \phi\) |
| 4. | \(\dfrac{V_{0} I_{0} \sin \phi}{2}\) |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The current through the primary of a step-down transformer with a turns-ratio of \(4\) is \(1.6~\text{A}\). The current in the secondary circuit is:
1. \(0.4~\text{A}\)
2. \(0.8~\text{A}\)
3. \(6.4~\text{A}\)
4. \(12.8~\text{A}\)
1. \(0.4~\text{A}\)
2. \(0.8~\text{A}\)
3. \(6.4~\text{A}\)
4. \(12.8~\text{A}\)
Subtopic: Transformer |
71%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Sinusoidal voltages are applied at \(X\) and \(Y\) so that the currents flowing into the capacitor at \(X\) and into the resistor at \(Y\) are equal and out of phase with each other. The RMS values of the voltages across the capacitor and the resistor are each equal to \(V_r\). The RMS value of \(V_X-V_Y\) is:
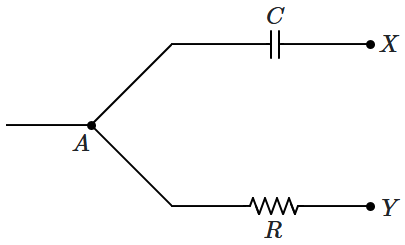
| 1. | zero | 2. | \(\sqrt 2 V_r \) |
| 3. | \(2 V_r\) | 4. | \(\dfrac{V_r}{\sqrt 2}\) |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The RMS voltage across the inductor is twice that across the capacitor, while the applied RMS voltage across the entire combination (i.e. \(V_{AX}\)) is \(V_r\). The RMS voltage across the capacitor is:
| 1. | \(\dfrac{V_r}{3}\) | 2. | \(\dfrac{2V_r}{3}\) |
| 3. | \(\dfrac{V_r}{2}\) | 4. | \(V_r\) |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
In the given scenario, the voltage, \(V_2 > V_1,\) and no current flow through the source on the left. The phase difference between the two sources is \(\phi.\)
Which of the following expressions correctly relates \(\phi\text{?}\)
| 1. | \(R\sin\phi= \dfrac{1}{\omega C}\) | 2. | \(R\cos\phi= \dfrac{1}{\omega C}\) |
| 3. | \(R\tan\phi= \dfrac{1}{\omega C}\) | 4. | \(R\cot\phi= \dfrac{1}{\omega C}\) |
Subtopic: Different Types of AC Circuits |
62%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Exactly identical voltages are imposed on the system at \(X, Y,\) and \(Z:V_m \sin \omega t\). The peak voltage at \(O\) is \(V_o\). Then:
1. \(V_o = V_m\)
2. \(V_o < V_m \)
3. \(V_o > V_m\)
4. any of the above can be possible.
1. \(V_o = V_m\)
2. \(V_o < V_m \)
3. \(V_o > V_m\)
4. any of the above can be possible.
Subtopic: Different Types of AC Circuits |
54%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A transformer has \(100\) turns in its primary. It has two secondary circuits: one with \(10\) turns and the other with \(20\) turns. The RMS voltage across the primary is \(30~\text{V}.\) The secondaries are connected to \(10~\Omega\) loads, as shown. Assuming no power loss, the RMS current in the primary is:
1. \(0.2~\text{A}\)
2. \(0.15~\text{A}\)
3. \(0.45~\text{A}\)
4. \(0.9~\text{A}\)
1. \(0.2~\text{A}\)
2. \(0.15~\text{A}\)
3. \(0.45~\text{A}\)
4. \(0.9~\text{A}\)
Subtopic: Transformer |
62%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Select Question Set:
© 2025 GoodEd Technologies Pvt. Ltd.