Select Question Set:
Q. No.An \(RC\) circuit is connected to a \(10\) V AC source and it is observed to supply a \(200\) mA current at a frequency of \(100\) kHz. The same resistance is now paired with an inductor \((L)\) in series and the same source supplies \(200\) mA current at a frequency of \(1\) kHz at the same operating voltage. If the circuit were made with the given \(L\text-C\text-R\) in series, the current will be a maximum when the frequency is \(f_o\). Then,
1.
\(f_o = \dfrac{10^3 + 10^5}{2}\) Hz
2.
\(f_o > \dfrac{10^3 + 10^5}{2}\) Hz
3.
\(f_o < \dfrac{10^3 + 10^5}{2}\) Hz
4.
\(f_o = {10^3 + 10^5}\) Hz
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
An AC source of emf \(100~\text{V}\) and frequency \(f= \dfrac{50}{\pi}\) Hz has an internal resistance \(100~\Omega\). A load resistance \(R_L\) is connected across the source. Maximum power is dissipated in the load, when:
| 1. | \(R_L = 100\sqrt 2~\Omega\) | 2. | \(R_L = \dfrac{100}{\sqrt 2}~\Omega \) |
| 3. | \(R_L = 100~\Omega\) | 4. | \(R_L = 200~\Omega\) |
Subtopic: Different Types of AC Circuits |
68%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
In this \(LCR\) circuit, it is observed that the current and the voltage are in phase with each other. When the capacitor is replaced by a short circuit, the phase difference becomes \(60^{\circ}.\)
Then:
Then:
| 1. | \(\dfrac{L}{C}=R^2 \) | 2. | \(\dfrac{L}{C}=2R^2\) |
| 3. | \(\dfrac{L}{C}=3R^2\) | 4. | \(\dfrac{L}{C}=\dfrac13R^2\) |
Subtopic: Different Types of AC Circuits |
65%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
In which of the following cases is the RMS voltage equal to the maximum voltage in magnitude?
1. A
2. A, B
3. A, B, C
4. None of the above
| (A) |  |
| (B) |  |
| (C) |  |
2. A, B
3. A, B, C
4. None of the above
Subtopic: RMS & Average Values |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A transformer has \(100\) turns in its primary. It has two secondary circuits: one with \(10\) turns and the other with \(20\) turns. The RMS voltage across the primary is \(30~\text{V}.\) The secondaries are connected to \(10~\Omega\) loads, as shown. Assuming no power loss, the RMS current in the primary is:
1. \(0.2~\text{A}\)
2. \(0.15~\text{A}\)
3. \(0.45~\text{A}\)
4. \(0.9~\text{A}\)
1. \(0.2~\text{A}\)
2. \(0.15~\text{A}\)
3. \(0.45~\text{A}\)
4. \(0.9~\text{A}\)
Subtopic: Transformer |
62%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Exactly identical voltages are imposed on the system at \(X, Y,\) and \(Z:V_m \sin \omega t\). The peak voltage at \(O\) is \(V_o\). Then:
1. \(V_o = V_m\)
2. \(V_o < V_m \)
3. \(V_o > V_m\)
4. any of the above can be possible.
1. \(V_o = V_m\)
2. \(V_o < V_m \)
3. \(V_o > V_m\)
4. any of the above can be possible.
Subtopic: Different Types of AC Circuits |
54%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
In the given scenario, the voltage, \(V_2 > V_1,\) and no current flow through the source on the left. The phase difference between the two sources is \(\phi.\)
Which of the following expressions correctly relates \(\phi\text{?}\)
| 1. | \(R\sin\phi= \dfrac{1}{\omega C}\) | 2. | \(R\cos\phi= \dfrac{1}{\omega C}\) |
| 3. | \(R\tan\phi= \dfrac{1}{\omega C}\) | 4. | \(R\cot\phi= \dfrac{1}{\omega C}\) |
Subtopic: Different Types of AC Circuits |
62%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The RMS voltage across the inductor is twice that across the capacitor, while the applied RMS voltage across the entire combination (i.e. \(V_{AX}\)) is \(V_r\). The RMS voltage across the capacitor is:
| 1. | \(\dfrac{V_r}{3}\) | 2. | \(\dfrac{2V_r}{3}\) |
| 3. | \(\dfrac{V_r}{2}\) | 4. | \(V_r\) |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Sinusoidal voltages are applied at \(X\) and \(Y\) so that the currents flowing into the capacitor at \(X\) and into the resistor at \(Y\) are equal and out of phase with each other. The RMS values of the voltages across the capacitor and the resistor are each equal to \(V_r\). The RMS value of \(V_X-V_Y\) is:
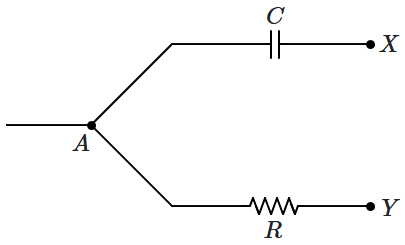
| 1. | zero | 2. | \(\sqrt 2 V_r \) |
| 3. | \(2 V_r\) | 4. | \(\dfrac{V_r}{\sqrt 2}\) |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The current through the primary of a step-down transformer with a turns-ratio of \(4\) is \(1.6~\text{A}\). The current in the secondary circuit is:
1. \(0.4~\text{A}\)
2. \(0.8~\text{A}\)
3. \(6.4~\text{A}\)
4. \(12.8~\text{A}\)
1. \(0.4~\text{A}\)
2. \(0.8~\text{A}\)
3. \(6.4~\text{A}\)
4. \(12.8~\text{A}\)
Subtopic: Transformer |
71%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Select Question Set:
© 2025 GoodEd Technologies Pvt. Ltd.