Two identical projectiles \(A,B\) launched 'towards' each other collide head-on, elastically at their highest points and return to their respective points of projection. Their angles of projection were \(\theta_A= 30^{\circ}\) and \(\theta_B= 45^{\circ}\). Their speeds are in the ratio \((v_A:v_{B}=)\)
1. \(2:3\)
2. \(3:2\)
3. \(\sqrt2:\sqrt3\)
4. \(\sqrt3:\sqrt2\)
1. \(2:3\)
2. \(3:2\)
3. \(\sqrt2:\sqrt3\)
4. \(\sqrt3:\sqrt2\)
A man drifting on a raft on a river observes a boat moving in the same direction at a relative speed which is \(3\) times the speed of the river's flow of \(3\) km/h. The boat overtakes him at a certain moment and reaches a point downstream after a time \(T_B\) while he reaches the same point after \(T_A=3 \) hr. Then, \(T_B= \)
| 1. | \(1\) hr | 2. | \(\dfrac12\)hr |
| 3. | \(\dfrac23\) hr | 4. | \(\dfrac34\) hr |
A projectile launched at an angle \(\theta\) is observed to move at an angle of \(45^\circ\) with the vertical (upward) at some point on its trajectory. If the launch angle \(\theta\) was increased, then the horizontal range:
| 1. | decreases |
| 2. | increases |
| 3. | first increases then decreases |
| 4. | first decreases then increases |
Consider a square carrom board \(ABCD\) of size \({3~ \text{ft}} \times 3~\text{ft}. \) A piece moves 'from' pocket \(A\) (close from a pocket), strikes side \(BC\) and then side \(AD\), and reaches pocket \(C\). If the piece is reflected perfectly from each side, then the ratio of the \(x,y\) components of velocity is given by \(\dfrac{v_x}{v_y}=\)
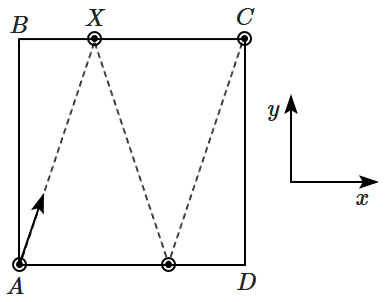
| 1. | \(2\) | 2. | \(\dfrac{1}{2}\) |
| 3. | \(3\) | 4. | \(\dfrac{1}{3}\) |
A projectile projected close to the earth's surface rises to a maximum height of \(H\) and has a horizontal range of \(d\). The horizontal velocity of the projectile is:
| 1. | \(\sqrt{2gd} \) | 2. | \(\sqrt{2gH} \) |
| 3. | \(\sqrt{\dfrac{gd^2}{2H}} \) | 4. | \(\sqrt{\dfrac{gd^2}{8H}}\) |
The angle between the vectors \(\widehat i+\widehat j \) and \(\widehat j+\widehat k \) is:
1. \(0^{\circ}\)
2. \(30^{\circ}\)
3. \(60^{\circ}\)
4. \(120^{\circ}\)
1. \(2u=v\)
2. \(3u=2v\)
3. \(2u = \sqrt 3 v\)
4. \(3u =\sqrt 2 v\)
| Assertion (A): | If two particles move with uniform accelerations in different directions, then their relative velocity changes in direction. |
| Reason (R): | Since the acceleration are in different directions, there is a relative acceleration and hence the relative velocity changes. |
| 1. | (A) is True but (R) is False. |
| 2. | (A) is False but (R) is True. |
| 3. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 4. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |

| 1. | \(a<\dfrac{2 g}{5}\) |
| 2. | \(\dfrac{2 g}{5}< a< \dfrac{3 g}{5}\) |
| 3. | \(\dfrac {3g} {5} <a<g\) |
| 4. | \(a = g \) |

| 1. | \(v_A~\text{cos}A=v_B~\text{cos}B\) |
| 2. | \(v_A~\text{sin}A=v_B~\text{sin}B\) |
| 3. | \(\dfrac{v_A}{\text{sin}A}=\dfrac{v_B}{\text{sin}B}\) |
| 4. | \(v_A~\text{tan}A=v_B~\text{tan}B\) |






