Select Chapter Topics:
Q. No.Given below are two statements:
| Assertion (A): | The impedance of a capacitance increases as the frequency increases. |
| Reason (R): | The charge and voltage across a capacitance are directly proportional to each other. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | (A) is False but (R) is True. |
Subtopic: Â AC vs DC |
 69%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The RMS-value of a time varying current is zero, during a given time interval. It can be concluded that, during this interval,
| 1. | the current is always zero |
| 2. | the current has identical positive and negative fluctuations |
| 3. | the current is positive for exactly half the time and negative for the remaining time |
| 4. | the current may be positive, negative or zero (during the interval) |
Subtopic: Â RMS & Average Values |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
In an \(\text{AC}\) circuit, the power dissipated in a resistance is found to \(P_1\) when a source voltage of \(V_1\) is connected across it. If the same resistance is connected in series with a capacitance and the same source is connected across the combination, the power in the resistance is found to be \(P_2=\dfrac{P_1}{2}.\) The phase difference between the voltage and the current is:
1. \(30^{\circ}\)
2. \(60^{\circ}\)
3. \(45^{\circ}\)
4. \(90^{\circ}\)
1. \(30^{\circ}\)
2. \(60^{\circ}\)
3. \(45^{\circ}\)
4. \(90^{\circ}\)
Subtopic: Â Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
An incandescent electric bulb rated at \(100~\text W\) for a \(220~\text V\)-AC household supply is connected to \(220~\text V\) DC supply. Treating the filament as a pure resistance, the bulb should:
| 1. | glow brighter |
| 2. | glow dimmer |
| 3. | glow the same |
| 4. | first glow brighter, then dims gradually |
Subtopic: Â Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
An alternating voltage of peak value \(300~\text V\) and a frequency \(50~\text{Hz}\) is applied across an inductor \(L=2~\text{mH}\) in a circuit. The induced voltage across the inductor has the peak value:
| 1. | equal to \(300~\text V\) |
| 2. | less than \(300~\text V\) |
| 3. | greater than \(300~\text V\) |
| 4. | zero |
Subtopic: Â Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
An \(RC\) circuit is connected to a \(10\) V AC source and it is observed to supply a \(200\) mA current at a frequency of \(100\) kHz. The same resistance is now paired with an inductor \((L)\) in series and the same source supplies \(200\) mA current at a frequency of \(1\) kHz at the same operating voltage. If the circuit were made with the given \(L\text-C\text-R\) in series, the current will be a maximum when the frequency is \(f_o\). Then,
| 1. | \(f_o = \dfrac{10^3 + 10^5}{2}\) Hz |
| 2. | \(f_o > \dfrac{10^3 + 10^5}{2}\) Hz |
| 3. | \(f_o < \dfrac{10^3 + 10^5}{2}\) Hz |
| 4. | \(f_o = {10^3 + 10^5}\) Hz |
Subtopic: Â Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The RMS voltage across the inductor is twice that across the capacitor, while the applied RMS voltage across the entire combination (i.e. \(V_{AX}\)) is \(V_r\). The RMS voltage across the capacitor is:
| 1. | \(\dfrac{V_r}{3}\) | 2. | \(\dfrac{2V_r}{3}\) |
| 3. | \(\dfrac{V_r}{2}\) | 4. | \(V_r\) |
Subtopic: Â Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The primary has \(100\) turns with \(100\) V RMS applied to it while the secondary has a total number of \(20\) turns, with the connection \(C\) made at the centre. The current \(i\) flowing towards \(C\) has the (RMS) value:
| 1. | \(2\) A | 2. | \(2\sqrt2\) A |
| 3. | \(\sqrt2\) A | 4. | zero |
Subtopic: Â Transformer |
 52%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Sinusoidal voltages are applied at \(X\) and \(Y\) so that the currents flowing into the capacitor at \(X\) and into the resistor at \(Y\) are equal and out of phase with each other. The RMS values of the voltages across the capacitor and the resistor are each equal to \(V_r\). The RMS value of \(V_X-V_Y\) is:
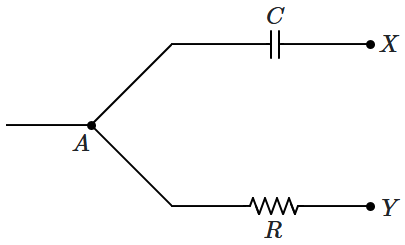
| 1. | zero | 2. | \(\sqrt 2 V_r \) |
| 3. | \(2 V_r\) | 4. | \(\dfrac{V_r}{\sqrt 2}\) |
Subtopic: Â Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
An alternating emf (AC) is applied across the circuit shown in the figure. Let \(V_{AX}\) be the voltage across the inductor \(L,\) and \(V_{XY}\) be the voltage across the resistor \(R.\) Let the angular frequency be \(\omega.\) The phase difference between \(V_{XY}\) and \(V_{AX}\):
| 1. | depends on the ratio \(\dfrac{\omega L}{R}\) |
| 2. | depends on the quantity \(\sqrt{(\omega L)^2+R^2}\) |
| 3. | depends on \(L\) and \(R,\) but not on \(\omega\) |
| 4. | is independent of \(L,R,\omega\) |
Subtopic: Â Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Select Chapter Topics:
© 2025 GoodEd Technologies Pvt. Ltd.