Select Chapter Topics:
Q. No.Given below are two statements:
| Statement I: | The gravitational force acting on a particle depends on the electric charge of the particle. |
| Statement II: | The gravitational force on an extended body can be calculated by assuming the body to be a particle 'concentrated' at its centre of mass and applying Newton's law of gravitation. |
| 1. | Statement I is incorrect and Statement II is correct. |
| 2. | Both Statement I and Statement II are correct. |
| 3. | Both Statement I and Statement II are incorrect. |
| 4. | Statement I is correct and Statement II is incorrect. |
Subtopic: Newton's Law of Gravitation |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A satellite is in a circular orbit around a planet, orbiting with a speed of \(2\) km/s. What is the minimum additional velocity that should be given to it, perpendicular to its motion, so that it escapes?
| 1. | \(2\) km/s | 2. | \(2\sqrt2\) km/s |
| 3. | \(2(\sqrt2-1)\) km/s | 4. | \(2(\sqrt2+1)\) km/s |
Subtopic: Escape velocity |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A block of mass \(m\) is slowly taken vertically upward over a large distance \(h\) in the earth's gravitational field, starting from its surface. The gravitational field at its final destination is \({\Large\frac{g}{27}},\) where \(g\) is the field at the earth's surface. The work done in the process is:
1. \(mgh\)
2. \(\Large\frac{mgh}{27}\)
3. \(\Large\frac{mgh}{\sqrt{27}}\)
4. \(\Large\frac{14mgh}{27}\)
1. \(mgh\)
2. \(\Large\frac{mgh}{27}\)
3. \(\Large\frac{mgh}{\sqrt{27}}\)
4. \(\Large\frac{14mgh}{27}\)
Subtopic: Gravitational Potential Energy |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Two particles of masses \(M,m\) are separated by a distance \(r.\) Their relative acceleration due to their mutual gravitational forces is (of magnitude):
| 1. | \(\Large\frac{2GMm}{r^2(M+m)}\) | 2. | \(\Large\frac{GMm}{r^2(M+m)}\) |
| 3. | \(\Large\frac{G(M\text - m)}{r^2}\) | 4. | \(\Large\frac{G(M\text + m)}{r^2}\) |
Subtopic: Acceleration due to Gravity |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A uniform solid sphere of mass \(M\) and radius \(R\) has a thin uniform ring of mass \(\dfrac{5M}{3}\) and radius \(\dfrac{4R}{3}\) around it. The two objects have a common centre \(O,\) and the axis of the ring \((PP')\) lies along a diameter of the sphere. Physical quantities associated with this system are mentioned in Column-I and their values in Column-II, but in a different order. Match them. Gravitational field is measured in units of \((GM/R^2),\) potential in units of \(\left(-\dfrac{GM}{R}\right)\) while potential energy is in units of \((-GM^2/R)\)
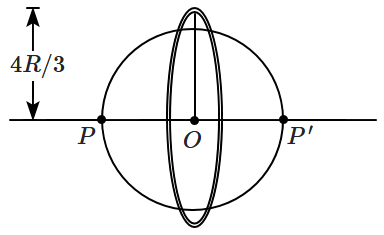
| Column-I | Column-II | ||
| \(\mathrm{(A)}\) | Gravitational potential energy (PE) of interaction between the sphere and the ring. | \(\mathrm{(I)}\) | \(1.25\) |
| \(\mathrm{(B)}\) | Gravitational potential at the common centre \((O)\) | \(\mathrm{(II)}\) | \(1.36\) |
| \(\mathrm{(C)}\) | Gravitational potential at \(P,\) a pole of the sphere. | \(\mathrm{(III)}\) | \(2\) |
| \(\mathrm{(D)}\) | Gravitational field at \(P,\) a pole of the sphere. | \(\mathrm{(IV)}\) | \(2.75\) |
| 1. | \(\mathrm{A\text-I,B\text-IV,C\text-III,D\text-II}\) |
| 2. | \(\mathrm{A\text-II,B\text-III,C\text-I,D\text-IV}\) |
| 3. | \(\mathrm{A\text-III,B\text-II,C\text-IV,D\text-I}\) |
| 4. | \(\mathrm{A\text-I,B\text-IV,C\text-II,D\text-III}\) |
Subtopic: Gravitational Potential |
50%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Three stars of identical masses \(m\) move around a central star of mass \(M\) in an orbit of radius \(r.\) The net gravitational force acting on any one of the orbiting stars equals:
| 1. | \(\dfrac{GMm}{r^2}+\dfrac{2Gm^2}{r^2}\) |
| 2. | \(\dfrac{GMm}{r^2}+\dfrac{\sqrt3Gm^2}{r^2}\) |
| 3. | \(\dfrac{GMm}{r^2}+\dfrac{Gm^2}{\sqrt3r^2}\) |
| 4. | \(\dfrac{GMm}{r^2}+\dfrac{2Gm^2}{\sqrt3r^2}\) |
Subtopic: Newton's Law of Gravitation |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
If a particle is projected vertically upward with a speed \(u,\) and rises to a maximum altitude \(h\) above the earth's surface then:
(\(g=\) acceleration due to gravity at the surface)
| 1. | \(h>\dfrac{u^2}{2g}\) |
| 2. | \(h=\dfrac{u^2}{2g}\) |
| 3. | \(h<\dfrac{u^2}{2g}\) |
| 4. | Any of the above may be true, depending on the earth's radius |
Subtopic: Acceleration due to Gravity |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The angular momentum of a planet of mass \(m,\) moving around the sun (mass: \(M\gg m\)) in an orbit of radius \(r\) is proportional to:
| 1. | \(mr\) | 2. | \(\dfrac{m}{r}\) |
| 3. | \(m\sqrt r\) | 4. | \(\dfrac{m}{\sqrt r}\) |
Subtopic: Kepler's Laws |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The gravitational potential energy of a particle of mass \(m\) increases by \(mgh,\) when it is raised through a height \(h\) in a uniform gravitational field "\(g\)". If a particle of mass \(m\) is raised through a height \(h\) in the earth's gravitational field (\(g\): the field on the earth's surface) and the increase in gravitational potential energy is \(U\), then:
| 1. | \(U > mgh\) |
| 2. | \(U < mgh\) |
| 3. | \(U = mgh\) |
| 4. | any of the above may be true depending on the value of \(h,\) considered relative to the radius of the earth. |
Subtopic: Gravitational Potential Energy |
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Two particles of masses \(m_1,~m_2\) are placed on the axis of a uniform circular ring of mass \(M\) and radius \(R,\) on opposite sides of the centre of the ring. The distances of \(m_1,~m_2\) from the centre of the ring are \(x_1,~x_2\) respectively, and \(x_1~ x_2 \ll R.\) The net force on the ring vanishes. Then,
| 1. | \(\dfrac{m_{1}}{x_{1}}=\dfrac{m_{2}}{x_{2}} \) | 2. | \(\dfrac{m_{1}}{x_{1}^{2}}=\dfrac{m_{2}}{x_{2}^{2}} \) |
| 3. | \(\dfrac{m_{1}}{x_{1}^{3}}=\dfrac{m_{2}}{x_{2}^{3}} \) | 4. | \(m_{1} x_{1}=m_{2} x_{2} \) |
Subtopic: Newton's Law of Gravitation |
52%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Select Chapter Topics:
© 2025 GoodEd Technologies Pvt. Ltd.