The rms speed of oxygen atoms is v. If the temperature is halved and the oxygen atoms combine to form oxygen molecules, then the rms speed will be:

1. $\frac{v}{\sqrt{2}}$

2. $v\sqrt{2}$

3. 2v

4. $\frac{v}{2}$

The mean free path of gas molecules depends on:
(\(d=\) molecular diameter)
1. \(d\)
2. \(d^2\)
3. \(d^{-2}\)
4. \(d^{-1}\)

Two thermally insulated vessels \(1\) and \(2\) are filled with air at temperatures \(\mathrm{T_1},\) \(\mathrm{T_2},\) volume \(\mathrm{V_1},\) \(\mathrm{V_2}\) and pressure \(\mathrm{P_1},\) \(\mathrm{P_2}\) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be:

If the mean free path of atoms is doubled, then the pressure of the gas will become:

1. \(\frac{P}{4}\)                   
2. \(\frac{P}{2}\)
3. \(\frac{P}{8}\)
4. \(P\)

The pressure in a diatomic gas increases from ${\mathrm{P}}_0$ to $3{\mathrm{P}}_0$, when its volume is increased from ${\mathrm{V}}_0$ $\mathrm{to}$ $2{\mathrm{V}}_0$. The increase in internal energy  will be:
     
1. $6{\mathrm{P}}_{\mathrm{o}}{\mathrm{V}}_0$

2. $8.5{\mathrm{P}}_{\mathrm{o}}{\mathrm{V}}_0$

3. $12.5{\mathrm{P}}_{\mathrm{o}}{\mathrm{V}}_0$

4. $14.5{\mathrm{P}}_{\mathrm{o}}{\mathrm{V}}_0$

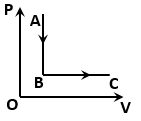
The figure shows a process for a gas in which pressure (P) and volume (V) of the gas change. If $C_1$ and $C_2$ are the molar heat capacities of the gas during the processes AB and BC respectively, then:

1. $C_1=C_2$

2. $C_1>C_2$

3. $C_1<C_2$

4. $C_1\le C_2$

The change in the internal energy of an ideal gas does not depend on?

The translational kinetic energy of \(n\) moles of a diatomic gas at absolute temperature \(T\) is given by:
1. \(\frac{5}{2}nRT\)
2. \(\frac{3}{2}nRT\)
3. \(5nRT\)
4. \(\frac{7}{2}nRT\)

Which of the following graphs, shows the variation of the mean kinetic energy \(E\) of an ideal gas molecule with temperature \(t ^\circ\text{C}?\)

1.		2.
3.		4.