Select Question Set:
Q. No.An electric motor of mass \(40~\text{kg}\) is mounted on four vertical springs each having a spring constant of \(4000~\text{Nm}^{-1}.\) The period with which the motor vibrates vertically is:
1. \(0.314~\text s\)
2. \(3.14~\text s\)
3. \(0.628~\text s\)
4. \(0.157~\text s\)
1. \(0.314~\text s\)
2. \(3.14~\text s\)
3. \(0.628~\text s\)
4. \(0.157~\text s\)
Subtopic: Combination of Springs |
64%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
Given below are two statements:
| Assertion (A): | The combination of \(y=\text{sin}\omega t+\text{cos}2\omega t\) is not a simple harmonic function even though it is periodic. |
| Reason (R): | All periodic functions satisfy the relation \( \dfrac{d^{2} y}{d t^{2}}=-k y \). |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
Subtopic: Simple Harmonic Motion |
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
\((\text{sin}\omega t+\text{cos}\omega t)\) is a periodic function, its time period will be:
| 1. | \(\dfrac{\pi}{\omega}\) | 2. | \(\dfrac{2\pi}{\omega}\) |
| 3. | \(\dfrac{1}{\omega}\) | 4. | \(\dfrac{\omega}{2\pi}\) |
Subtopic: Types of Motion |
86%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A particle moves in the \(\mathrm{XY}\text-\text{plane}\) according to the equation \(\vec{r}=\left ( 5\hat{i}+3\hat{j} \right )\text{sin}(2t).\) The motion of the particle is along:
| 1. | a straight line and is periodic. |
| 2. | a circle and is non-periodic. |
| 3. | an ellipse and is periodic. |
| 4. | a parabola and is non-periodic. |
Subtopic: Simple Harmonic Motion |
52%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
When a periodic force \(\vec{F_1}\) acts on a particle, the particle oscillates according to the equation \(x=A\sin\omega t\). Under the effect of another periodic force \(\vec{F_2}\), the particle oscillates according to the equation \(y=B\sin(\omega t+\frac{\pi}{2})\). The amplitude of oscillation when the force (\(\vec{F_1}+\vec{F_2}\)) acts are:
| 1. | \(A+B\) | 2. | \(\sqrt{A^2+B^2}\) |
| 3. | \(\large\frac{\sqrt{A^2+B^2}}{2}\) | 4. | \(\sqrt{AB}\) |
Subtopic: Simple Harmonic Motion |
91%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The total mechanical energy of a linear harmonic oscillator is \(600~\text J.\) At the mean position, its potential energy is \(100~\text J.\) The minimum potential energy of the oscillator is:
1. \(50~\text J\)
2. \(500~\text J\)
3. \(0\)
4. \(100~\text J\)
Subtopic: Energy of SHM |
72%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The time period of a simple pendulum in a stationary lift is \(T.\) If the lift accelerates upward with an acceleration of \(\dfrac g 6\) (where \(g\) is the acceleration due to gravity), then the time period of the pendulum would be:
| 1. | \(\sqrt{\dfrac{6}{5}} ~T \) | 2. | \(\sqrt{\dfrac{5}{6}} ~T\) |
| 3. | \(\sqrt{\dfrac{6}{7}}~T\) | 4. | \(\sqrt{\dfrac{7}{6}} ~T\) |
Subtopic: Angular SHM |
79%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A block of mass \(M\) is connected to a spring constant \(k.\) It oscillates on the frictionless inclined surface as shown in the figure. The time period of oscillation is:
| 1. | \(T=2 \pi \sqrt{\dfrac{M}{k}}\) | 2. | \(T=2 \pi \sqrt{\dfrac{k}{M}}\) |
| 3. | \(T=\dfrac{1}{2 \pi} \sqrt{\dfrac{k}{M}}\) | 4. | \(T=2 \pi \sqrt{\dfrac{M}{k}} \sin \theta\) |
Subtopic: Spring mass system |
81%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
The acceleration-time graph of a particle undergoing SHM is shown in the figure. Then,
| 1. | the velocity of the particle at point 2 is zero |
| 2. | velocity at point 3 is zero |
| 3. | velocity at point 2 is +ve and maximum |
| 4. | both (2) & (3) |
Subtopic: Simple Harmonic Motion |
73%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The (displacement-time) graph of a particle executing SHM is shown in the figure. Then:
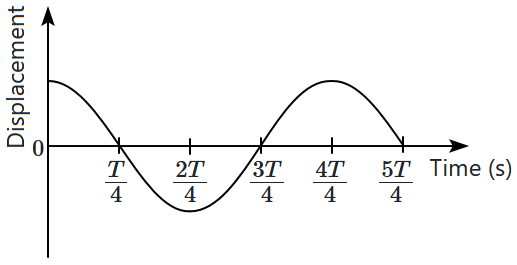
| (a) | the force is zero at \(t=\dfrac{3T}{4}\) |
| (b) | the acceleration is maximum at \(t=\dfrac{4T}{4}\) |
| (c) | the velocity is maximum at \(t=\dfrac{T}{4}\) |
| (d) | the potential energy is equal to the kinetic energy of oscillation at \(t=\dfrac{T}{2}\) |
| 1. | (a), (b) and (d) only | 2. | (a), (b) and (c) only |
| 3. | (b), (c) and (d) only | 4. | (c) and (d) only |
Subtopic: Simple Harmonic Motion |
68%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Select Question Set:
© 2025 GoodEd Technologies Pvt. Ltd.