Two ideal gases have the same number of molecules per unit volume and the radii of their molecules are \(r\) and \(3r\) respectively. The ratio of their mean free path in identical containers will be:

1.	\(3:1\)	2.	\(9:1\)
3.	\(1:1\)	4.	\(1:4\)

When a large bubble rises from the bottom of a lake to the surface, its radius doubles. The atmospheric pressure is equal to that of a column of water of height H. The depth of the lake is:

1. H

2. 2H

3. 7H

4. 8H

If at a pressure of \(10^6\) dyne/cm², one gram of nitrogen occupies \(2\times10^4\) c.c. volume, then the average energy of a nitrogen molecule in erg is:

Which of the following graphs, shows the variation of the mean kinetic energy \(E\) of an ideal gas molecule with temperature \(t ^\circ\text{C}?\)

1.		2.
3.		4.

The translational kinetic energy of \(n\) moles of a diatomic gas at absolute temperature \(T\) is given by:
1. \(\frac{5}{2}nRT\)
2. \(\frac{3}{2}nRT\)
3. \(5nRT\)
4. \(\frac{7}{2}nRT\)

The change in the internal energy of an ideal gas does not depend on?

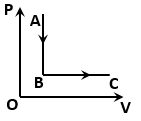
The figure shows a process for a gas in which pressure (P) and volume (V) of the gas change. If $C_1$ and $C_2$ are the molar heat capacities of the gas during the processes AB and BC respectively, then:

1. $C_1=C_2$

2. $C_1>C_2$

3. $C_1<C_2$

4. $C_1\le C_2$

The pressure in a diatomic gas increases from ${\mathrm{P}}_0$ to $3{\mathrm{P}}_0$, when its volume is increased from ${\mathrm{V}}_0$ $\mathrm{to}$ $2{\mathrm{V}}_0$. The increase in internal energy  will be:
     
1. $6{\mathrm{P}}_{\mathrm{o}}{\mathrm{V}}_0$

2. $8.5{\mathrm{P}}_{\mathrm{o}}{\mathrm{V}}_0$

3. $12.5{\mathrm{P}}_{\mathrm{o}}{\mathrm{V}}_0$

4. $14.5{\mathrm{P}}_{\mathrm{o}}{\mathrm{V}}_0$

Without change in temperature, a gas is forced in a smaller volume. Its pressure increases because its molecules:

The mean free path for a gas, with molecular diameter \(d\) and number density \(n,\) can be expressed as:
1. \( \dfrac{1}{\sqrt{2} n \pi {d}^2} \)

2. \( \dfrac{1}{\sqrt{2} n^2 \pi {d}^2} \)

3. \(\dfrac{1}{\sqrt{2} n^2 \pi^2 d^2} \)

4. \( \dfrac{1}{\sqrt{2} n \pi {d}}\)