A gas undergoes an isothermal process. The specific heat capacity of the gas in the process is:
1.
infinity
2.
\(0.5\)
3.
zero
4.
\(1\)
An ideal gas undergoes a thermodynamic process described by the equation:
\(PV^2=C,\)
where \(C\) is a constant. The gas transitions from an initial state \((P_1, V_1, T_1)\) to a final state \((P_2, V_2, T_2).\) Which of the following statements is correct?
| 1. | \(\text{If}~P_1>P_2,~\text{then}~T_1<T_2 \) |
| 2. | \(\text{If}~V_2>V_1,~\text{then}~T_2>T_1\) |
| 3. | \(\text{If}~V_2>V_1,~\text{then}~T_2<T_1\) |
| 4. | \(\text{If}~P_1>P_2,~\text{then}~V_1>V_2\) |

| 1. | \(4\) | 2. | \(1\) |
| 3. | \(2\) | 4. | \(3\) |
1. \(200^\circ \mathrm{C}\)
2. \(27^\circ \mathrm{C}\)
3. \(15^\circ \mathrm{C}\)
4. \(100^\circ \mathrm{C}\)

| 1. | \(200\) J | 2. | zero |
| 3. | \(400\) J | 4. | \(600\) J |
The graph below shows the processes involved in a Carnot engine.
For the two isotherms 1 and 2, the temperature of isotherm 1 is:
1. Equal to the temperature of isotherm 2
2. More than the temperature of isotherm 2
3. Less than the temperature of isotherm 2
4. Sometimes more & sometimes less than the temperature of isotherm 2
The graph given below shows variation of specific heat capacity of water versus temperature.
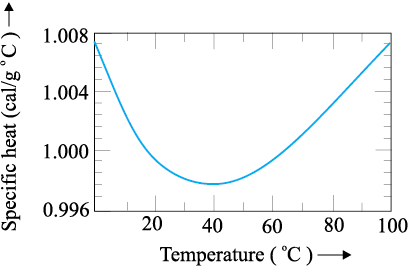
From the graph given above, we can conclude that:
1. Specific heat capacity always increases
2. Specific heat capacity always decreases
3. Specific heat capacity never changes
4. Specific heat capacity first decreases and then increases
The \((P\text{-}V)\) diagram for an ideal gas in a piston-cylinder assembly undergoing a thermodynamic process is shown in the figure. The process is:
| 1. | adiabatic | 2. | isochoric |
| 3. | isobaric | 4. | isothermal |
The efficiency of a Carnot engine depends upon:
1. the temperature of the sink only.
2. the temperatures of the source and the sink.
3. the volume of the cylinder of the engine.
4. the temperature of the source only.

| 1. | \(30~\text J\) | 2. | \(-90~\text J\) |
| 3. | \(-60~\text J\) | 4. | zero |








