The \((P\text{-}V)\) diagram for an ideal gas in a piston-cylinder assembly undergoing a thermodynamic process is shown in the figure. The process is:

1.
adiabatic
2.
isochoric
3.
isobaric
4.
isothermal

The efficiency of a Carnot engine depends upon:
1. the temperature of the sink only.
2. the temperatures of the source and the sink.
3. the volume of the cylinder of the engine.
4. the temperature of the source only.
Q. 5 Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of the final pressure of gas in B to that of gas in A is:
a.
b.
c.
d.
Consider a heat engine as shown in the figure. are heat added to and heat taken from respectively, in one cycle of the engine. W is the mechanical work done on the engine.
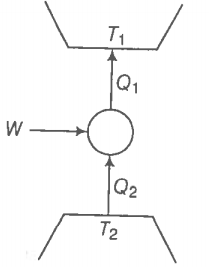
If W > 0, then possibilities are:
Choose the correct alternatives:
1. (b, c)
2. (a, d)
3. (b, d)
4. (a, c)
Consider a cycle followed by an engine (figure).
1 to 2 is isothermal,
2 to 3 is adiabatic,
3 to 1 is adiabatic.
Such a process does not exist, because:
| (a) | heat is completely converted to mechanical energy in such a process, which is not possible. |
| (b) | In this process, mechanical energy is completely converted to heat, which is not possible. |
| (c) | curves representing two adiabatic processes don’t intersect. |
| (d) | curves representing an adiabatic process and an isothermal process don't intersect. |
Choose the correct alternatives:
| 1. | (a), (b) | 2. | (a), (c) |
| 3. | (b), (c) | 4. | (c), (d) |
The figure shows the \((P\text-V)\) diagram of an ideal gas undergoing a change of state from \(A\) to \(B.\) Four different paths \(\mathrm{I, II, III}\) and \(\mathrm{IV},\) as shown in the figure, may lead to the same change of state.

| (a) | The change in internal energy is the same in cases \(\mathrm{IV}\) and \(\mathrm{III}\) but not in cases \(\mathrm{I}\) and \(\mathrm{II}.\) |
| (b) | The change in internal energy is the same in all four cases. |
| (c) | The work done is maximum in case \(\mathrm{I}.\) |
| (d) | The work done is minimum in case \(\mathrm{II}.\) |
Which of the following options contains only correct statements?
| 1. | (b), (c) and (d) only | 2. | (a) and (d) only |
| 3. | (b) and (c) only | 4. | (a), (c) and (d) only |
| (a) | \(dU = 0 \) | (b) | \(dQ = 0\) |
| (c) | \(dQ = dU \) | (d) | \(dQ = dW\) |
| 1. | (a), (b), (c) | 2. | (a), (d) |
| 3. | (b), (c), (d) | 4. | (a), (c), (d) |
| (a) | The increase in temperature of an iron rod by hammering it. |
| (b) | A gas in a small container at a temperature \(T_1\) is brought in contact with a big reservoir at a higher temperature \(T_2\) which increases the temperature of the gas. |
| (c) | A quasi-static isothermal expansion of an ideal gas in a cylinder fitted with a frictionless piston. |
| (d) | An ideal gas is enclosed in a piston-cylinder arrangement with adiabatic walls. A weight \(w\) is added to the piston, resulting in the compression of gas. |
| 1. | (a), (b), (c) | 2. | (a), (d) |
| 3. | (b), (c), (d) | 4. | (a), (b), (d) |
(\(s\) is the specific heat of copper)
| 1. | \(T = \dfrac{T_{1} + T_{2} + T_{3}}{3}\) |
| 2. | \(T = \dfrac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{M_{1} + M_{2} + M_{3}}\) |
| 3. | \(T = \dfrac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{3 \left(\right. M_{1} + M_{2} + M_{3} \left.\right)}\) |
| 4. | \(T = \dfrac{M_{1} T_{1} s + M_{2} T_{2} s + M_{3} T_{3} s}{M_{1} + M_{2} + M_{3}}\) |
Consider the \((P\text-V)\) diagram for an ideal gas shown in the figure.

Out of the following diagrams, which figure represents the \((T\text-P)\) diagram?
| 1. |  |
2. |  |
| 3. |  |
4. |  |







