Select Question Set:
Q. No.The current in an inductor of self-inductance \(4~\text{H}\) changes from \(4~ \text{A}\) to \(2~\text{A}\) in \(1~ \text s\). The emf induced in the coil is:
1. \(-2~\text{V}\)
2. \(2~\text{V}\)
3. \(-4~\text{V}\)
4. \(8~\text{V}\)
1. \(-2~\text{V}\)
2. \(2~\text{V}\)
3. \(-4~\text{V}\)
4. \(8~\text{V}\)
Subtopic: Self - Inductance |
85%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The dimensions of mutual inductance \((M)\) are:
| 1. | \(\left[M^2LT^{-2}A^{-2}\right]\) | 2. | \(\left[MLT^{-2}A^{2}\right]\) |
| 3. | \(\left[M^{2}L^{2}T^{-2}A^{2}\right]\) | 4. | \(\left[ML^{2}T^{-2}A^{-2}\right]\) |
Subtopic: Mutual Inductance |
75%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
An inductor coil of self-inductance \(10~\text{H}\) carries a current of \(1~\text{A}\). The magnetic field energy stored in the coil is:
| 1. | \(10~\text{J}\) | 2. | \(2.5~\text{J}\) |
| 3. | \(20~\text{J}\) | 4. | \(5~\text{J}\) |
Subtopic: Self - Inductance |
86%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A small square loop of wire of side \(\ell \) is placed inside a large square loop of wire \(L\) \((L\gg l).\) Both loops are coplanar and their centres coincide at point \(O\) as shown in the figure. The mutual inductance of the system is:
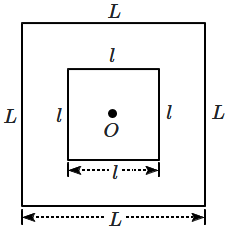
| 1. | \(\dfrac{2\sqrt{2}\mu _{0}L^{2}}{\pi \ell}\) | 2. | \(\dfrac{\mu_{0} \ell^{2}}{2 \sqrt{2} \pi {L}} \) |
| 3. | \(\dfrac{2 \sqrt{2} \mu_{0} \ell^{2}}{\pi {L}} \) | 4. | \(\dfrac{\mu_{0} L^{2}}{2 \sqrt{2} \pi \ell}\) |
Subtopic: Mutual Inductance |
71%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A straight wire \(AB\) of length \(L\) rotates about \(A,\) with an angular speed \(\omega.\) A constant magnetic field \(\mathbf B\) acts into the plane, as shown.
| Assertion (A): | The average induced electric field within the wire has a magnitude of \(\dfrac12B\omega L.\) |
| Reason (R): | The induced electric field is the motional EMF per unit length, and the motional EMF is \(\dfrac12B\omega L^2.\) |
| 1. | (A) is True but (R) is False. |
| 2. | (A) is False but (R) is True. |
| 3. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 4. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
Subtopic: Motional emf |
55%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A square loop with a side length of \(10~\text{cm}\) is placed vertically in the east-west plane. A uniform magnetic field of \(0.1~\text{T}\) is applied across the plane of the loop in the northeast direction. The magnetic flux linked with the loop is:
| 1. | \(\sqrt2\times10^{-2}\) Wb | 2. | \(\sqrt2\times10^{-3}\) Wb |
| 3. | \(\dfrac{1}{\sqrt{2}}\times10^{-2}\) Wb | 4. | \(\dfrac{1}{\sqrt{2}}\times10^{-3}\) Wb |
Subtopic: Magnetic Flux |
74%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A circular coil of radius \(10\) cm, \(100\) turns is placed with its plane perpendicular to the horizontal component of earth's magnetic field \((=3.0\times 10^{-5}~\text{T})\). It is rotated about its vertical diameter through \(180^\circ\) in \(0.314\) s. What is the magnitude of emf induced in the coil?
| 1. | \(3\times 10^{-4}\) V | 2. | \(6\times 10^{-4}\) V |
| 3. | \(6\times 10^{-5}\) V | 4. | \(6\times 10^{-6}\) V |
Subtopic: Faraday's Law & Lenz Law |
51%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
The magnetic flux through a coil perpendicular to its plane is varying according to the relation \(\phi = (5t^3 + 4t^{2} +2t-5)~\text{Wb}.\) If the resistance of the coil is \(5~\Omega,\) then the induced current through the coil at \(t=2~\text s\) will be:
1. \(15.6~\text A\)
2. \(16.6~\text A\)
3. \(17.6~\text A\)
4. \(18.6~\text A\)
1. \(15.6~\text A\)
2. \(16.6~\text A\)
3. \(17.6~\text A\)
4. \(18.6~\text A\)
Subtopic: Faraday's Law & Lenz Law |
86%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
The magnetic flux linked to a circular coil of radius \(R\) is given by:
\(\phi=2t^3+4t^2+2t+5\) Wb.
What is the magnitude of the induced EMF in the coil at \(t=5\) s?
1. \(108\) V
2. \(197\) V
3. \(150\) V
4. \(192\) V
Subtopic: Faraday's Law & Lenz Law |
87%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A straight conductor of length \(6~\text{m},\) placed along the \(z\text-\)axis, begins to move along the positive \(x\text- \)axis with a velocity of \(5\) m/s in a magnetic field \(\vec {B}=(0.2 \hat{i}+0.1 \hat{j}) ~\text{T}.\) The induced EMF across the conductor is:
1. \(6\) V
2. \(3\) V
3. \(1\) V
4. \(5\) V
1. \(6\) V
2. \(3\) V
3. \(1\) V
4. \(5\) V
Subtopic: Motional emf |
75%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
Select Question Set:
© 2025 GoodEd Technologies Pvt. Ltd.