The potential energy of a simple harmonic oscillator, when the particle is halfway to its endpoint, will be:
1. \(\frac{2E}{3}\)
2. \(\frac{E}{8}\)
3. \(\frac{E}{4}\)
4. \(\frac{E}{2}\)
1. \(\frac{2E}{3}\)
2. \(\frac{E}{8}\)
3. \(\frac{E}{4}\)
4. \(\frac{E}{2}\)
A particle of mass \(m\) oscillates with simple harmonic motion between points \(x_1\) and \(x_2\), the equilibrium position being \(O\). Its potential energy is plotted. It will be as given below in the graph:
| 1. |  |
2. | 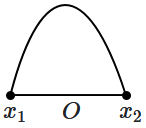 |
| 3. |  |
4. |  |
When a mass is suspended separately by two different springs, in successive order, then the time period of oscillations is \(t _1\) and \(t_2\) respectively. If it is connected by both springs as shown in the figure below, then the time period of oscillation becomes \(t_0.\) The correct relation between \(t_0,\) \(t_1\) & \(t_2\) is:

1.
2.
3.
4.
A spring elongates by a length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached to the mass 'M' and then released. The new time period of oscillation will be:
1. \(2 \pi \sqrt{\frac{\left(\right. M + m \left.\right) l}{Mg}}\)
2. \(2 \pi \sqrt{\frac{ml}{Mg}}\)
3. \(2 \pi \sqrt{L / g}\)
4. \(2 \pi \sqrt{\frac{Ml}{\left(\right. m + M \left.\right) g}}\)
A spring is stretched by \(5~\text{cm}\) by a force \(10~\text{N}\). The time period of the oscillations when a mass of \(2~\text{kg}\) is suspended by it is:
1. \(3.14~\text{s}\)
2. \(0.628~\text{s}\)
3. \(0.0628~\text{s}\)
4. \(6.28~\text{s}\)
Two spherical bobs of masses \(M_A\) and \(M_B\) are hung vertically from two strings of length \(l_A\) and \(l_B\) respectively. If they are executing SHM with frequency as per the relation \(f_A=2f_B,\) Then:
1. \(l_A = \frac{l_B}{4}\)
2. \(l_A= 4l_B\)
3. \(l_A= 2l_B~\&~M_A=2M_B\)
4. \(l_A= \frac{l_B}{2}~\&~M_A=\frac{M_B}{2}\)
| 1. | \(0.01~\text{Hz}\) | 2. | \(0.02~\text{Hz}\) |
| 3. | \(0.03~\text{Hz}\) | 4. | \(0.04~\text{Hz}\) |
The equation of a simple harmonic wave is given by \(y=3\sin \frac{\pi}{2}(50t-x)\) where \(x \) and \(y\) are in meters and \(t\) is in seconds. The ratio of maximum particle velocity to the wave velocity is:
| 1. | \(\frac{3\pi}{2}\) | 2. | \(3\pi\) |
| 3. | \(\frac{2\pi}{3}\) | 4. | \(2\pi\) |
A spring-mass system oscillates in a car. If the car accelerates on a horizontal road, the frequency of oscillation will:
1. increase
2. decrease
3. remain same
4. become zero
The (displacement-time) graph of a particle executing SHM is shown in the figure. Then:
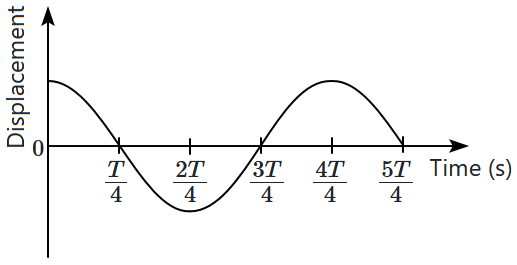
| (a) | the force is zero at \(t=\dfrac{3T}{4}\) |
| (b) | the acceleration is maximum at \(t=\dfrac{4T}{4}\) |
| (c) | the velocity is maximum at \(t=\dfrac{T}{4}\) |
| (d) | the potential energy is equal to the kinetic energy of oscillation at \(t=\dfrac{T}{2}\) |
| 1. | (a), (b) and (d) only | 2. | (a), (b) and (c) only |
| 3. | (b), (c) and (d) only | 4. | (c) and (d) only |






