Q. No.All the surfaces are smooth and springs are ideal. If a block of mass \(m\) is given the velocity \(v_0\) in the right direction, then the time period of the block shown in the figure will be:
1. \(\frac{12l}{v_0}\)
2. \(\frac{2l}{v_0}+ \frac{3\pi}{2}\sqrt{\frac{m}{k}}\)
3. \(\frac{4l}{v_0}+ \frac{3\pi}{2}\sqrt{\frac{m}{k}}\)
4. \( \frac{\pi}{2}\sqrt{\frac{m}{k}}\)
A spring is stretched by \(5~\text{cm}\) by a force \(10~\text{N}\). The time period of the oscillations when a mass of \(2~\text{kg}\) is suspended by it is:
1. \(3.14~\text{s}\)
2. \(0.628~\text{s}\)
3. \(0.0628~\text{s}\)
4. \(6.28~\text{s}\)
1. \(\pi\)
2. \(\frac{\pi}{2}\)
3. \(\frac{\pi}{4}\)
4. \(2\pi\)
1. \(1:\sqrt{3}\)
2. \(1:1\)
3. \(2:1\)
4. \(\sqrt{3}:2\)
A spring having a spring constant of \(1200\) N/m is mounted on a horizontal table as shown in the figure. A mass of \(3\) kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of \(2.0\) cm and released. The frequency of oscillations will be:
| 1. | \(3.0~\text{s}^{-1}\) | 2. | \(2.7~\text{s}^{-1}\) |
| 3. | \(1.2~\text{s}^{-1}\) | 4. | \(3.2~\text{s}^{-1}\) |
An ideal spring with spring-constant K is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially un-stretched. Then the maximum extension in the spring will be:
1. 4 Mg/K
2. 2 Mg/K
3. Mg/K
4. Mg/2K
A body of mass \(m\) is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass \(m\) is slightly pulled down and released, it oscillates with a time period of \(3~\text{s}\). When the mass \(m\) is increased by \(1~\text{kg}\), the time period of oscillations becomes \(5~\text{s}\). The value of \(m\) in \(\text{kg}\) is:
1. \(\dfrac{3}{4}\)
2. \(\dfrac{4}{3}\)
3. \(\dfrac{16}{9}\)
4. \(\dfrac{9}{16}\)
| 1. |  |
2. |  |
| 3. |  |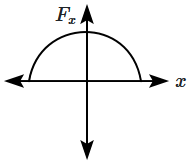
4. |  |
A spring elongates by a length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached to the mass 'M' and then released. The new time period of oscillation will be:
1. \(2 \pi \sqrt{\frac{\left(\right. M + m \left.\right) l}{Mg}}\)
2. \(2 \pi \sqrt{\frac{ml}{Mg}}\)
3. \(2 \pi \sqrt{L / g}\)
4. \(2 \pi \sqrt{\frac{Ml}{\left(\right. m + M \left.\right) g}}\)
| 1. | \(\dfrac{4\pi}{10}~\text{s}\) | 2. | \(\dfrac{3\pi}{10}~\text{s}\) |
| 3. | \(\dfrac{2\pi}{7}~\text{s}\) | 4. | \(\dfrac{\pi}{10}~\text{s}\) |
© 2025 GoodEd Technologies Pvt. Ltd.