- 1(current)
Q. No.The graph between \(\dfrac1u\) and \(\dfrac1v\) for a thin convex lens in order to determine its focal length is plotted as shown in the figure. The refractive index of the lens is \(1.5\) and both surfaces have the same radius of curvature \(R.\) The value of \(R\) will be: (where \(u\) = object distance, \(v\) = image distance)
1. \(10~\text{cm}\)
2. \(20~\text{cm}\)
3. \(30~\text{cm}\)
4. \(40~\text{cm}\)
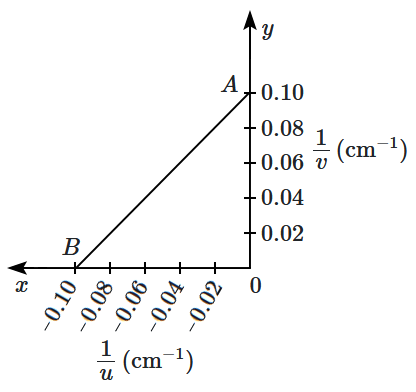
1. \(10~\text{cm}\)
2. \(20~\text{cm}\)
3. \(30~\text{cm}\)
4. \(40~\text{cm}\)
Subtopic: Â Lens Makers' Formula |
 67%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
Double-convex lenses are to be manufactured from a glass of refractive index \(1.55\) with both faces of the same radius of curvature. What is the radius of curvature required, if the focal length is to be \(20~\text{cm}\)?
1. \(20~\text{cm}\)
2. \(22~\text{cm}\)
3. \(24~\text{cm}\)
4. \(15~\text{cm}\)
Subtopic: Â Lens Makers' Formula |
 80%
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
Links
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The power of a lens (biconvex) is \(1.25~\text{m}^{-1}\) in a particular medium. The refractive index of the lens is \(1.5\) and the radii of curvature are \(20\) cm and \(40\) cm respectively. The refractive index of the surrounding medium is:
| 1. | \(1\) | 2. | \(\dfrac 97\) |
| 3. | \(\dfrac 3 2\) | 4. | \(\dfrac 4 3\) |
Subtopic: Â Lens Makers' Formula |
 55%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.