Q. No.The law of conservation of angular momentum is valid when:
| 1. | The net force is zero and the net torque is non-zero | 2. | The net force is non-zero and the net torque is non zero |
| 3. | Net force may or may not be zero and net torque is zero | 4. | Both force and torque must be zero |
Two particles of mass \(5~\text{kg}\) and \(10~\text{kg}\) respectively are attached to the two ends of a rigid rod of length \(1~\text{m}\) with negligible mass. The centre of mass of the system from the \(5~\text{kg}\) particle is nearly at a distance of:
1. \(50~\text{cm}\)
2. \(67~\text{cm}\)
3. \(80~\text{cm}\)
4. \(33~\text{cm}\)
A particle starting from rest moves in a circle of radius \(r\). It attains a velocity of \(v_0~\text{m/s}\) on completion of \(n\) rounds. Its angular acceleration will be:
1. \( \dfrac{v_0}{n} ~\text{rad} / \text{s}^2\)
2. \( \dfrac{v_0^2}{2 \pi {nr}^2}~ \text{rad} / \text{s}^2 \)
3. \( \dfrac{v_0^2}{4 \pi {n}{r}^2}~ \text{rad} / \text{s}^2 \)
4. \( \dfrac{v_0^2}{4 \pi {nr}} ~\text{rad} / \text{s}^2 \)
| 1. | zero | 2. | \(1~\text{m}\) |
| 3. | \(2~\text{m}\) | 4. | \(5~\text{m}\) |
A string is wrapped along the rim of a wheel of the moment of inertia \(0.10~\text{kg-m}^2\) and radius \(10~\text{cm}.\) If the string is now pulled by a force of \(10~\text N,\) then the wheel starts to rotate about its axis from rest. The angular velocity of the wheel after \(2~\text s\) will be:
| 1. | \(40~\text{rad/s}\) | 2. | \(80~\text{rad/s}\) |
| 3. | \(10~\text{rad/s}\) | 4. | \(20~\text{rad/s}\) |
Three identical spheres, each of mass \(M\), are placed at the corners of a right-angle triangle with mutually perpendicular sides equal to \(2~\text{m}\) (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of the centre of mass.
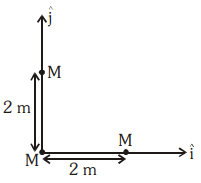
| 1. | \(2( \hat{i}+ \hat{j})\) | 2. | \(( \hat{i}+ \hat{j})\) |
| 3. | \({2 \over 3}( \hat{i}+ \hat{j})\) | 4. | \({4 \over 3}( \hat{i}+ \hat{j})\) |
An object flying in the air with velocity \((20 \hat{i}+25 \hat{j}-12 \hat{k})\) suddenly breaks into two pieces whose masses are in the ratio of \(1:5.\) The smaller mass flies off with a velocity \((100 \hat{i}+35 \hat{j}+8 \hat{k})\). The velocity of the larger piece will be:
1. \( 4 \hat{i}+23 \hat{j}-16 \hat{k}\)
2. \( -100 \hat{i}-35 \hat{j}-8 \hat{k} \)
3. \( 20 \hat{i}+15 \hat{j}-80 \hat{k} \)
4. \( -20 \hat{i}-15 \hat{j}-80 \hat{k}\)
The angular speed of the wheel of a vehicle is increased from \(360~\text{rpm}\) to \(1200~\text{rpm}\) in \(14\) seconds. Its angular acceleration will be:
1. \(2\pi ~\text{rad/s}^2\)
2. \(28\pi ~\text{rad/s}^2\)
3. \(120\pi ~\text{rad/s}^2\)
4. \(1 ~\text{rad/s}^2\)
The mass per unit length of a non-uniform rod of length \(L\) is given by \(\mu =λx^{2}\) where \(\lambda\) is a constant and \(x\) is the distance from one end of the rod. The distance between the centre of mass of the rod and this end is:
| 1. | \(\frac{L}{2}\) | 2. | \(\frac{L}{4}\) |
| 3. | \(\frac{3L}{4}\) | 4. | \(\frac{L}{3}\) |
A mass \(m\) moves in a circle on a smooth horizontal plane with velocity \(v_0\) at a radius \(R_0.\) The mass is attached to a string that passes through a smooth hole in the plane, as shown in the figure.
The tension in the string is increased gradually and finally, \(m\) moves in a circle of radius \(\frac{R_0}{2}.\) The final value of the kinetic energy is:
1. \( m v_0^2 \)
2. \( \frac{1}{4} m v_0^2 \)
3. \( 2 m v_0^2 \)
4. \( \frac{1}{2} m v_0^2\)
© 2025 GoodEd Technologies Pvt. Ltd.