- 1(current)
Q. No.A long solenoid of diameter \(0.1\) m has \(2 \times 10^4\) turns per meter. At the center of the solenoid, a coil of \(100\) turns and radius \(0.01\) m is placed with its axis coinciding with the solenoid axis. The current in the solenoid reduces at a constant rate to \(0\) A from \(4\) A in \(0.05\) s. If the resistance of the coil is \(10\pi^2~\Omega\), then the total charge flowing through the coil during this time is:
1. \(16~\mu \text{C}\)
2. \(32~\mu \text{C}\)
3. \(16\pi~\mu \text{C}\)
4. \(32\pi~\mu \text{C}\)
| 1. | \(\dfrac{R^2_1}{R_2}\) | 2. | \(\dfrac{R^2_2}{R_1}\) |
| 3. | \(\dfrac{R_1}{R_2}\) | 4. | \(\dfrac{R_2}{R_1}\) |
| 1. | \(\left[M^2LT^{-2}A^{-2}\right]\) | 2. | \(\left[MLT^{-2}A^{2}\right]\) |
| 3. | \(\left[M^{2}L^{2}T^{-2}A^{2}\right]\) | 4. | \(\left[ML^{2}T^{-2}A^{-2}\right]\) |
Two circular coils can be arranged in any of the three situations shown in the figure. Their mutual inductance will be
1. Maximum in situation (A)
2. Maximum in situation (B)
3. Maximum in situation (C)
4. The same in all situations
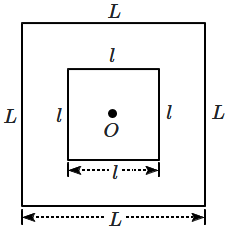
| 1. | \(\dfrac{2\sqrt{2}\mu _{0}L^{2}}{\pi \ell}\) | 2. | \(\dfrac{\mu_{0} \ell^{2}}{2 \sqrt{2} \pi {L}} \) |
| 3. | \(\dfrac{2 \sqrt{2} \mu_{0} \ell^{2}}{\pi {L}} \) | 4. | \(\dfrac{\mu_{0} L^{2}}{2 \sqrt{2} \pi \ell}\) |
| 1. | current flowing in the two coils |
| 2. | material of the wires of the coils |
| 3. | the relative position and orientation of the two coils |
| 4. | rate of change in current in the two coils |
1. \(\dfrac{MkT^2}{4R}\)
2. \(\dfrac{2MkT^2}{R}\)
3. \(\dfrac{MkT^2}{2R}\)
4. Zero
Read the passage given below and answer the given question.
Mutual Inductance is the phenomenon of induced emf in a coil, due to a change of current in the neighbouring coil. The amount of mutual inductance that links one coil to another depends very much on the relative positioning of the two coils, their geometry, and the relative separation between them. Mutual inductance between the two coils increases times if the coils are wound over an iron core of relative permeability \(\mu_r.\)
A short solenoid of radius \(a,\) number of turns per unit length \(n_1,\) and length \(L\) is kept coaxially inside a very long solenoid of radius \(b,\) number of turns per unit length \(n_2.\) What is the mutual inductance of the system?
| 1. | \(\mu_0 \pi b^2n_1n_2L\) | 2. | \(\mu_0 \pi a^2n_1n_2L^2\) |
| 3. | \(\mu_0 \pi a^2n_1n_2L\) | 4. | \(\mu_0 \pi b^2n_1n_2L^2\) |
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.