- 1(current)
Q. No.The figure given below shows the displacement and time, \((x\text -t)\) graph of a particle moving along a straight line:
The correct statement, about the motion of the particle, is:
| 1. | the particle moves at a constant velocity up to a time \(t_0\) and then stops. |
| 2. | the particle is accelerated throughout its motion. |
| 3. | the particle is accelerated continuously for time \(t_0\) then moves with constant velocity. |
| 4. | the particle is at rest. |
Subtopic: Â Graphs |
 77%
Level 2: 60%+
NEET - 2022
Hints
The displacement-time \((s\text-t)\) graphs of two moving particles \(A~\text{and}~B\) make angles of \(30^\circ\) and \(45^\circ\) with the \(x\text-\)axis as shown in the figure. The ratio of their respective velocity \(\left(\dfrac{v_A}{v_B}\right) \) is:
1. \(1: \sqrt{3}\)
2. \(\sqrt{3}: 1\)
3. \(1:1\)
4. \(1:2\)
1. \(1: \sqrt{3}\)
2. \(\sqrt{3}: 1\)
3. \(1:1\)
4. \(1:2\)
Subtopic: Â Graphs |
 75%
Level 2: 60%+
NEET - 2022
Hints
Which one of the following displacement-time graph represents two moving objects \(P\) and \(Q\) with zero relative velocity?
| 1. |  |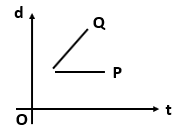
2. |  |
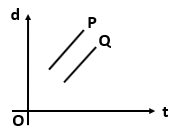| 3. |  |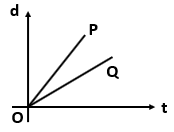
4. |  |
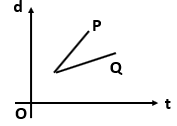Subtopic: Â Graphs |
 86%
Level 1: 80%+
Hints
Links
The position (\(x\)) of a particle in a straight line motion is given by \(x = 2 + 10 t - 5 t^{2}~\text{m}\). Its velocity (\(v\)) is best represented by?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Subtopic: Â Graphs |
 77%
Level 2: 60%+
Hints
Links
Subtopic: Â Graphs |
 81%
Level 1: 80%+
NEET - 2022
Hints
A ball is thrown vertically upward with a certain velocity from the surface of the earth and after some time it returns back to the earth. The velocity-time (\(v\text-t\)) graph for the entire journey is given by:
| 1. |  |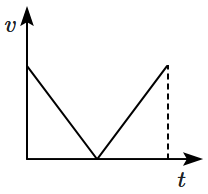
2. |  |
| 3. |  |
4. |  |
Subtopic: Â Graphs |
 58%
Level 3: 35%-60%
Please attempt this question first.
Hints
Please attempt this question first.
Which of the following position-time \((x\text-t)\) graphs may be possible corresponding to given velocity-time \((v\text-t)\) graph?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Subtopic: Â Graphs |
 69%
Level 2: 60%+
Please attempt this question first.
Hints
Please attempt this question first.
Which of the following statements is true about the motion depicted in the diagram?
| 1. | The acceleration is constant and non-zero. |
| 2. | The velocity changes suddenly during the motion. |
| 3. | The velocity is positive throughout. |
| 4. | All of the above are true. |
Subtopic: Â Graphs |
 65%
Level 2: 60%+
Hints
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.