An AC-voltage is applied across the ends \(A,B\) of the circuit shown in the figure, the RMS voltage being \(V_0\). It is observed that the RMS currents in all the three branches are equal to \(\dfrac{V_0}{R}\). The total current entering at \(A\) equals:

| 1. | \(\dfrac{V_0}{R}\) | 2. | \(\sqrt{2}\dfrac{V_0}{R}\) |
| 3. | \(\Big(\sqrt{2}+1\Big)\dfrac{V_0}{R}\) | 4. | \(\sqrt{3}\dfrac{V_0}{R}\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
The charge flowing through a resistance \(R\) is given by,
\(q = A\sin\omega t+B\cos\omega t\)
The heat produced in the resistance over a very long time \(\Delta t\) (much greater than \(T = 2\pi/ \omega\)) is:
1. \(\omega^{2}\left(A^{2}+B^{2}\right) R \Delta t\)
2. \(\omega^{2}\left(A^{2}-B^{2}\right) R \Delta t\)
3. \(\dfrac{1}{2} \omega^{2}\left(A^{2}+B^{2}\right) R \Delta t\)
4. \(\dfrac{1}{2} \omega^{2}\left(A^{2}-B^{2}\right) R \Delta t\)

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
An inductor \(200\) mH, capacitor \(20~\mu\text{F}\) and a resistance of \(200~\Omega\) are connected in series across a source of emf, \(E = (20~\text{V})\sin(500t)\), where \(t\) is in second. The power loss in the circuit is:
1. \(2~\text{W}\)
2. \(1~\text{W}\)
3. \(0.5~\text{W}\)
4. \(0.25~\text{W}\)

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
\(e=V_0\sin(wt)\)
and the current, \(i\) is
\(i=I_0\cos(wt-\phi).\) The average power dissipated per cycle is:
| 1. | \(V_{0} I_{0} {\cos\phi}\) |
| 2. | \(\dfrac{V_{0} I_{0} \cos \phi}{2}\) |
| 3. | \(V_{0} I_{0} \sin \phi\) |
| 4. | \(\dfrac{V_{0} I_{0} \sin \phi}{2}\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
1. \(0.4~\text{A}\)
2. \(0.8~\text{A}\)
3. \(6.4~\text{A}\)
4. \(12.8~\text{A}\)

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
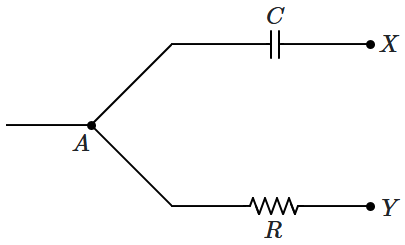
1. zero
2. \(\sqrt 2 V_r \)
3. \(2 V_r\)
4. \(\dfrac{V_r}{\sqrt 2}\)

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.

| 1. | \(\dfrac{V_r}{3}\) | 2. | \(\dfrac{2V_r}{3}\) |
| 3. | \(\dfrac{V_r}{2}\) | 4. | \(V_r\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
In the given scenario, the voltage, \(V_2 > V_1,\) and no current flow through the source on the left. The phase difference between the two sources is \(\phi.\)

Which of the following expressions correctly relates \(\phi\text{?}\)
| 1. | \(R\sin\phi= \dfrac{1}{\omega C}\) | 2. | \(R\cos\phi= \dfrac{1}{\omega C}\) |
| 3. | \(R\tan\phi= \dfrac{1}{\omega C}\) | 4. | \(R\cot\phi= \dfrac{1}{\omega C}\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.

1. \(V_o = V_m\)
2. \(V_o < V_m \)
3. \(V_o > V_m\)
4. any of the above can be possible.

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.

1. \(0.2~\text{A}\)
2. \(0.15~\text{A}\)
3. \(0.45~\text{A}\)
4. \(0.9~\text{A}\)

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.






