A transformer has \(100\) turns in its primary. It has two secondary circuits: one with \(10\) turns and the other with \(20\) turns. The RMS voltage across the primary is \(30~\text{V}.\) The secondaries are connected to \(10~\Omega\) loads, as shown. Assuming no power loss, the RMS current in the primary is:

1. \(0.2~\text{A}\)
2. \(0.15~\text{A}\)
3. \(0.45~\text{A}\)
4. \(0.9~\text{A}\)

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
| 1. | \(f_o = \dfrac{10^3 + 10^5}{2}\) Hz |
| 2. | \(f_o > \dfrac{10^3 + 10^5}{2}\) Hz |
| 3. | \(f_o < \dfrac{10^3 + 10^5}{2}\) Hz |
| 4. | \(f_o = {10^3 + 10^5}\) Hz |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
| 1. | \(R_L = 100\sqrt 2~\Omega\) | 2. | \(R_L = \dfrac{100}{\sqrt 2}~\Omega \) |
| 3. | \(R_L = 100~\Omega\) | 4. | \(R_L = 200~\Omega\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.

Then:
| 1. | \(\dfrac{L}{C}=R^2 \) | 2. | \(\dfrac{L}{C}=2R^2\) |
| 3. | \(\dfrac{L}{C}=3R^2\) | 4. | \(\dfrac{L}{C}=\dfrac13R^2\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
| (A) |  |
| (B) |  |
| (C) |  |
2. A, B
3. A, B, C
4. None of the above

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.

1. \(V_o = V_m\)
2. \(V_o < V_m \)
3. \(V_o > V_m\)
4. any of the above can be possible.

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
In the given scenario, the voltage, \(V_2 > V_1,\) and no current flow through the source on the left. The phase difference between the two sources is \(\phi.\)

Which of the following expressions correctly relates \(\phi\text{?}\)
| 1. | \(R\sin\phi= \dfrac{1}{\omega C}\) | 2. | \(R\cos\phi= \dfrac{1}{\omega C}\) |
| 3. | \(R\tan\phi= \dfrac{1}{\omega C}\) | 4. | \(R\cot\phi= \dfrac{1}{\omega C}\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.

| 1. | \(\dfrac{V_r}{3}\) | 2. | \(\dfrac{2V_r}{3}\) |
| 3. | \(\dfrac{V_r}{2}\) | 4. | \(V_r\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
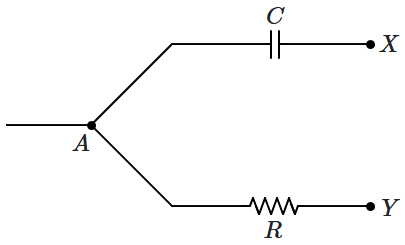
| 1. | zero | 2. | \(\sqrt 2 V_r \) |
| 3. | \(2 V_r\) | 4. | \(\dfrac{V_r}{\sqrt 2}\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
1. \(0.4~\text{A}\)
2. \(0.8~\text{A}\)
3. \(6.4~\text{A}\)
4. \(12.8~\text{A}\)

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.






