An organ pipe filled with a gas at \(27^\circ \text{C}\) resonates at \(400\) Hz in its fundamental mode. If it is filled with the same gas at \(90^\circ \text{C},\) the resonance frequency at the same mode will be:
1.
\(420\) Hz
2.
\(440\) Hz
3.
\(484\) Hz
4.
\(512\) Hz
A string of length \(l\) is fixed at both ends and is vibrating in second harmonic. The amplitude at antinode is \(2\) mm. The amplitude of a particle at a distance \(l/8\) from the fixed end is:
1. \(2\sqrt2~\text{mm}\)
2. \(4~\text{mm}\)
3. \(\sqrt2~\text{mm}\)
4. \(2\sqrt3~\text{mm}\)
1. \(1:2\)
2. \(1:1\)
3. \(\sqrt{2}:1\)
4. \(1:\sqrt{2}\)
| 1. | \(3:1\) | 2. | \(1:2\) |
| 3. | \(2:1\) | 4. | \(1:3\) |
| 1. | \(8:9\) | 2. | \(9:7\) |
| 3. | \(9:8\) | 4. | \(7:9\) |
1. 13 dB
2. 9 dB
3. 25 dB
4. Remains the same
A pipe, \(30.0\) cm long, is open at both ends.
| (i) | Which harmonic mode of the pipe resonates a \(1.1\) kHz source? |
| (ii) | Will resonance with the same source be observed if one end of the pipe is closed? |
Take the speed of sound in air as \(330\) m s–1.
| (i) | (ii) | |
| 1. | First | No |
| 2. | Second | No |
| 3. | First | Yes |
| 4. | Second | Yes |
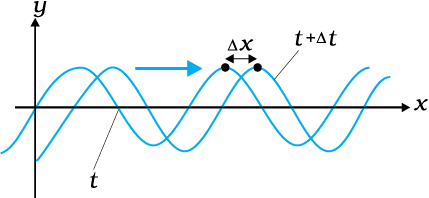
The given diagram shows the progression of a harmonic wave from time t to t + where the crest of the wave displaces by . Then the speed of the wave will be:
A rocket is moving at a speed of \(200\) ms–1 towards a stationary target. While moving, it emits a wave of frequency \(1000\) Hz. Some of the sound reaching the target gets reflected back to the rocket as an echo. The frequency of the sound as detected by the target and the frequency of the echo as detected by the rocket respectively are: (speed of sound = \(330\) m/s)
1. \(4080\) Hz and \(2540\) Hz
2. \(1000\) Hz and \(1000\) Hz
3. \(2540\) Hz and \(4080\) Hz
4. \(2540\) Hz and \(2540\) Hz
Two sitar strings A and B playing the note ‘Dha’ are slightly out of tune and produce beats of frequency \(5\) Hz. The tension of the string B is slightly increased and the beat frequency is found to decrease to \(3\) Hz. What is the original frequency of B if the frequency of A is \(427\) Hz?
1. \(432\) Hz
2. \(424\) Hz
3. \(430\) Hz
4. \(422\) Hz







