+91-8527521718
Signup | Login
Select Question Set:
filter
Test-14 (waves)
Q. No.

If the absolute temperature increases by \(1\%\), the frequency of an organ pipe will:
1. increase by \(1\%\) 2. decrease by \(1\%\)
3. increase by \(0.5\%\) 4. decrease by \(0.5\%\)

Subtopic:  Speed of Sound |
 74%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

A heavy uniform rope \(PQ\) is suspended from the ceiling. The lowest end of the rope is given a sharp transverse "shake" (or vibration) so as to cause a pulse. This pulse travels upward. As it travels upward, its speed:
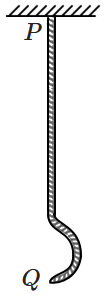
1. increases 2. decreases
3. first increases and then decreases 4. remains constant
Subtopic:  Travelling Wave on String |
 57%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

When two identical loudspeakers playing the same frequency are placed equidistant from an observer, a sound of \(60\) dB is heard if the sources are in phase with each other. However, if the two speakers are out of phase, no sound is heard. If the speakers are played with a phase difference of \(90^\circ,\) the sound heard will be:
1. \(30\sqrt2\) dB
2. \((60+\sqrt2)\) dB
3. \(57\) dB
4. \(60\sqrt2\) dB
Subtopic:  Pressure Wave in Sound |
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
The equation of vibration of a taut string, fixed at both ends, is given by; \(y=(3~\text{mm})~\text{cos}\left(\dfrac{\pi x}{10~\text{cm}}\right)~\text{sin}(800\pi~\text{s}^{-1}{t}).\) The positions of the nodes are:
1. \(x= 0~\text{cm}, 10~\text{cm}, 20~\text{cm},....\)
2. \(x= 0~\text{cm}, 20~\text{cm}, 40~\text{cm},....\)
3. \(x= 5~\text{cm}, 10~\text{cm}, 15~\text{cm},....\)
4. \(x= 5~\text{cm}, 15~\text{cm}, 25~\text{cm},....\)
Subtopic:  Beats |
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Sinusoidal sound waves of the same frequency travelling in air along the \(x\)-axis and the \(y\)-axis arrive in phase with each other at the origin. Their amplitudes are equal to \(A\) (each). The amplitude of the vibration at the origin is:
               
1. \(A\)
2. \(\sqrt 2A\)
3. \(2A\)
4. \((2+\sqrt2)A\)
Subtopic:  Wave Motion |
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

The fundamental frequencies of a closed pipe and an open pipe are identical. The first overtone for the closed pipe is \(f_c\) and for the open pipe is \(f_o.\) Their ratio \(\dfrac{f_c}{f_o}\) is:
1. \(1\) 2. \(1/2\)
3. \(2/3\) 4. \(3/2\)
Subtopic:  Standing Waves |
 70%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
The square of the speed of sound in a mono-atomic gas is proportional to:
1. its internal energy 
2. its internal energy per unit volume 
3. its internal energy per unit mass 
4. its internal energy per unit temperature  
Subtopic:  Speed of Sound |
 58%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

A string fixed at both ends is under tension \(T.\) It has a length \(L,\) and mass \(m.\) The fundamental frequency of the vibration is: 
1. \(\dfrac{ 1}{2L} \sqrt {\dfrac{T}{m}}\)
2. \(\dfrac{1}{4 L} \sqrt{\dfrac{T}{m}}\)
3. \(\dfrac{1}{2} \sqrt{\dfrac{TL}{2m}}\)
4. \(\dfrac{1}{2} \sqrt{\dfrac{T}{m L}}\)
Subtopic:  Travelling Wave on String |
 57%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

The first overtone of a closed pipe has a frequency \(f_c.\) A frequency that is \(2f_c\) can be excited from an open pipe of the same length but vibrating in its: 
1. \(2^{\text{nd}}\) harmonic 2. \(3^{\text{rd}}\) harmonic
3. \(6^{\text{th}}\) harmonic 4. \(12^{\text{th}}\) harmonic
Subtopic:  Standing Waves |
 67%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
The equation of vibration of a taut string, fixed at both ends, is given by:    \(y=(4~\text{mm})~\cos\left(\dfrac{\pi x}{30~\text{cm}}\right)~\sin\Big(400\pi s^{-1}t\Big) \)
At which points is the amplitude equal to \(2\) mm?
1. \(x = \) \(10\) cm, \(20\) cm, \(30\) cm, \(40\) cm
2. \(x=\) \(10\) cm, \(15\) cm, \(30\) cm, \(45\) cm
3. \(x =\) \(10\) cm, \(20\) cm, \(40\) cm, \(80\) cm
4. \(x = \) \(10\) cm, \(20\) cm, \(40\) cm, \(50\) cm
Subtopic:  Standing Waves |
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Select Question Set:
filter
Test-14 (waves)
Q. No.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions

© 2025 GoodEd Technologies Pvt. Ltd.