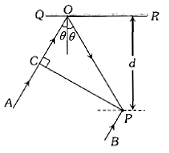
In the adjacent diagram, CP represents a wavefront and AO & BP, the corresponding two rays. Find the condition on for constructive interference at P between the ray BP and reflected ray OP
1.
2.
3.
4.
In Young's double slit experiment with slit seperation d, a monochromatic light of wavelength is used. The angular seperation of the fringes is
1.
2.
3.
4.
Two slits in Young's experiment have widths in the ratio 1:25. The ratio of intensity at the maximum and minimum in the interferance pattern, is
1.
2.
3.
4.
At the first minimum adjacent to the central maximum of a single-slit differaction pattern, the phase difference between the Huygen's wavelet from the edge of the slit and the wavelet from the midpoint of the slit is
1. radian
2.
3. radian
4. radian
Two beams of light will not give rise to an interference pattem, if
1. They are coherent
2. They have the same wavelength
3. They are linearly polarized perpendicular to each other
4. They are not monochromatic
Young's experiment is performed in air and then performed in water, the fringe width
1. Will remain same
2. Will decrease
3. Will increase
4. Will be infinite
In the Young's double slit experiment, if the phase difference between the two waves interfering at a point is , the intensity at that point can be expressed by the expression
1.
2.
3.
4.
Where A and B depend upon the amplitude of the two waves.
A slit of width a is illuminated by white light. For red light , the first minima is obtained at . Then the value of a will be
1.
2.
3. 1.24 microns
4.
Two waves originating from source S1 and S2 having zero phase difference and common wavelength will show completely destructive interference at a point P if is
1. 5
2. 3 / 4
3. 2
4. 11 / 2
The Brewster angle for the glass-air interface is 54.74o. lf a ray of light going from air to glass strikes at an angle of incidence 45o, then the angle of refraction is
(Hint: tan 54.74o = )
1. 60o
2. 30o
3. 25o
4. 54.74o






