+91-8527521718
Signup | Login
  • 1(current)
Q. No.
Two cars \(A\) and \(B\) start moving along the same straight road, from the same point, simultaneously. The first car \((A)\) accelerates uniformly to a maximum speed of \(v_0\) and then decelerates uniformly to a stop. The second car \((B)\) accelerates uniformly to the same maximum speed \(v_0\) and then decelerates uniformly to a stop. The acceleration of \(A\) is twice that of \(B,\) and they both spend the same total time during the motion. Then,
(A) distance travelled by \(A\) = distance travelled by \(B\)
(B) acceleration time of \(A\) = \(\dfrac12\) acceleration time of \(B\)
(C) relative velocity of \(A\) with respect to \(B\) is always positive
(D) deceleration time of \(A\) = \(2×\) deceleration time of \(B\)

Choose the correct option from the given ones:
1. (A) is True.
2. (A), (B) are True.
3. (A), (B), (C) are True.
4. (B), (C), (D) are True.
Subtopic:  Acceleration |
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

A balloon ascends upward with a constant upward velocity \(5\) m/s. At the same time it is being pushed to the right by the wind with a speed that is proportional to its height \((y)\):    \(v_\text{right}=2y\)
where the units are in SI. The acceleration of the balloon is: 
1. zero
2. \(10\) m/s2 to right
3. \(5\) m/s2 to right
4. \(10\) m/s2 upward
Subtopic:  Acceleration |
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

A small particle slides up and down along a smooth path \(ABC~(\angle B=90^{\circ}), \) under the action of gravity, coming to a stop briefly at the highest points \((A,C)\) of the path \(ABC.\) The path is rounded at \(B \) to facilitate the back and forth motion. The time taken for the particle to go from \(A\) to \(C\) is
      
 
1. \(\sqrt{\dfrac{2h}{g}}(\sin\theta+\cos\theta) \)
2. \(\sqrt{\dfrac{2h}{g}}(\sin^2\theta+\cos^2\theta) \)
3. \(\sqrt{\dfrac{2h}{g}}\left(\dfrac1{\sin\theta}+\dfrac1{\cos\theta}\right) \)
4. \(\sqrt{\dfrac{2h}{g}}\left(\dfrac1{\sin^2\theta\cdot \cos^2\theta}\right) \)
Subtopic:  Acceleration |
 54%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
The velocity-time graph of a particle, moving along a straight time, is shown in the figure. The curve, when plotted, takes the form of a 'circle'. The magnitude of the average acceleration of the particle is:
                   
1. \(1\) m/s2 
2. \(2\) m/s2
3. less than \(1\) m/s2
4. greater than \(2\) m/s2
Subtopic:  Acceleration |
 61%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

A particle moves along a straight line such that its velocity is proportional to the square root of its displacement. Its acceleration is:
1. zero
2. constant
3. proportional to time
4. proportional to displacement
Subtopic:  Acceleration |
 70%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Two particles move with constant speeds of \(3~\text{m/s}\) and \(5~\text{m/s}\) along the periphery of a square \(ABCD\) of side \(2~\text{m}\) (as shown). They start from \(A\) at the same time.

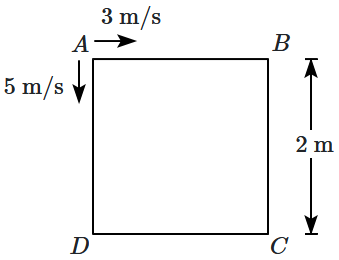
Their average accelerations, over the motion till they meet for the first time, are:
1. \(3\sqrt2~\text{m/s}^2,5\sqrt2~\text{m/s}^2 \)
2. \(3~\text{m/s}^2,5~\text{m/s}^2 \)
3. \(3\sqrt2~\text{m/s}^2,10~\text{m/s}^2 \)
4. \(6~\text{m/s}^2,10~\text{m/s}^2 \)
Subtopic:  Acceleration |
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
  • 1(current)
Q. No.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions

© 2025 GoodEd Technologies Pvt. Ltd.