Test-7 (Gravitation) Gravitation Physics NEET Practice Questions, MCQs, Past Year Questions (PYQs), NCERT Questions, Question Bank, Class 11 and Class 12 Questions, and PDF solved with answers

Statement I:	The gravitational force acting on a particle depends on the electric charge of the particle.
Statement II:	The gravitational force on an extended body can be calculated by assuming the body to be a particle 'concentrated' at its centre of mass and applying Newton's law of gravitation.

1.	Statement I is incorrect and Statement II is correct.
2.	Both Statement I and Statement II are correct.
3.	Both Statement I and Statement II are incorrect.
4.	Statement I is correct and Statement II is incorrect.

Add Note

Subtopic: Newton's Law of Gravitation |

From NCERT

Other Reason

Highlight in NCERT

Select Color:

Add Note (Optional):

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Upgrade Your Plan

Upgrade now and unlock your full question bank experience with daily practice.

Q2:

A satellite is in a circular orbit around a planet, orbiting with a speed of \(2\) km/s. What is the minimum additional velocity that should be given to it, perpendicular to its motion, so that it escapes?

1.	\(2\) km/s	2.	\(2\sqrt2\) km/s
3.	\(2(\sqrt2-1)\) km/s	4.	\(2(\sqrt2+1)\) km/s

Add Note

Subtopic: Escape velocity |

From NCERT

Other Reason

Highlight in NCERT

Select Color:

Add Note (Optional):

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Upgrade Your Plan

Upgrade now and unlock your full question bank experience with daily practice.

Q3:

A block of mass \(m\) is slowly taken vertically upward over a large distance \(h\) in the earth's gravitational field, starting from its surface. The gravitational field at its final destination is \({\Large\frac{g}{27}},\) where \(g\) is the field at the earth's surface. The work done in the process is:
1. \(mgh\)
2. \(\Large\frac{mgh}{27}\)
3. \(\Large\frac{mgh}{\sqrt{27}}\)
4. \(\Large\frac{14mgh}{27}\)

Add Note

Subtopic: Gravitational Potential Energy |

From NCERT

Other Reason

Highlight in NCERT

Select Color:

Add Note (Optional):

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Upgrade Your Plan

Upgrade now and unlock your full question bank experience with daily practice.

Q4:

Two particles of masses \(M,m\) are separated by a distance \(r.\) Their relative acceleration due to their mutual gravitational forces is (of magnitude):

1.	\(\Large\frac{2GMm}{r^2(M+m)}\)	2.	\(\Large\frac{GMm}{r^2(M+m)}\)
3.	\(\Large\frac{G(M\text - m)}{r^2}\)	4.	\(\Large\frac{G(M\text + m)}{r^2}\)

Add Note

Subtopic: Acceleration due to Gravity |

From NCERT

Other Reason

Highlight in NCERT

Select Color:

Add Note (Optional):

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Upgrade Your Plan

Upgrade now and unlock your full question bank experience with daily practice.

Q5:

A uniform solid sphere of mass \(M\) and radius \(R\) has a thin uniform ring of mass \(\dfrac{5M}{3}\) and radius \(\dfrac{4R}{3}\) around it. The two objects have a common centre \(O,\) and the axis of the ring \((PP')\) lies along a diameter of the sphere. Physical quantities associated with this system are mentioned in Column-I and their values in Column-II, but in a different order. Match them. Gravitational field is measured in units of \((GM/R^2),\) potential in units of \(\left(-\dfrac{GM}{R}\right)\) while potential energy is in units of \((-GM^2/R)\)

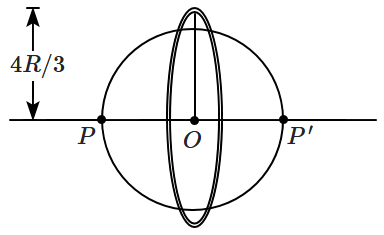
Column-I		Column-II
\(\mathrm{(A)}\)	Gravitational potential energy (PE) of interaction between the sphere and the ring.	\(\mathrm{(I)}\)	\(1.25\)
\(\mathrm{(B)}\)	Gravitational potential at the common centre \((O)\)	\(\mathrm{(II)}\)	\(1.36\)
\(\mathrm{(C)}\)	Gravitational potential at \(P,\) a pole of the sphere.	\(\mathrm{(III)}\)	\(2\)
\(\mathrm{(D)}\)	Gravitational field at \(P,\) a pole of the sphere.	\(\mathrm{(IV)}\)	\(2.75\)

1.	\(\mathrm{A\text-I,B\text-IV,C\text-III,D\text-II}\)
2.	\(\mathrm{A\text-II,B\text-III,C\text-I,D\text-IV}\)
3.	\(\mathrm{A\text-III,B\text-II,C\text-IV,D\text-I}\)
4.	\(\mathrm{A\text-I,B\text-IV,C\text-II,D\text-III}\)

Add Note

Subtopic: Gravitational Potential |

50%

From NCERT

Other Reason

Highlight in NCERT

Select Color:

Add Note (Optional):

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Upgrade Your Plan

Upgrade now and unlock your full question bank experience with daily practice.

Q6:

Three stars of identical masses \(m\) move around a central star of mass \(M\) in an orbit of radius \(r.\) The net gravitational force acting on any one of the orbiting stars equals:

1.	\(\dfrac{GMm}{r^2}+\dfrac{2Gm^2}{r^2}\)
2.	\(\dfrac{GMm}{r^2}+\dfrac{\sqrt3Gm^2}{r^2}\)
3.	\(\dfrac{GMm}{r^2}+\dfrac{Gm^2}{\sqrt3r^2}\)
4.	\(\dfrac{GMm}{r^2}+\dfrac{2Gm^2}{\sqrt3r^2}\)

Add Note

Subtopic: Newton's Law of Gravitation |

From NCERT

Other Reason

Highlight in NCERT

Select Color:

Add Note (Optional):

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Upgrade Your Plan

Upgrade now and unlock your full question bank experience with daily practice.

Q7:

If a particle is projected vertically upward with a speed \(u,\) and rises to a maximum altitude \(h\) above the earth's surface then:
(\(g=\) acceleration due to gravity at the surface)

1.	\(h>\dfrac{u^2}{2g}\)
2.	\(h=\dfrac{u^2}{2g}\)
3.	\(h<\dfrac{u^2}{2g}\)
4.	Any of the above may be true, depending on the earth's radius

Add Note

Subtopic: Acceleration due to Gravity |

From NCERT

Other Reason

Highlight in NCERT

Select Color:

Add Note (Optional):

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Upgrade Your Plan

Upgrade now and unlock your full question bank experience with daily practice.

Q8:

The angular momentum of a planet of mass \(m,\) moving around the sun (mass: \(M\gg m\)) in an orbit of radius \(r\) is proportional to:

1.	\(mr\)	2.	\(\dfrac{m}{r}\)
3.	\(m\sqrt r\)	4.	\(\dfrac{m}{\sqrt r}\)

Add Note

Subtopic: Kepler's Laws |

From NCERT

Other Reason

Highlight in NCERT

Select Color:

Add Note (Optional):

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Upgrade Your Plan

Upgrade now and unlock your full question bank experience with daily practice.

Q9:

The gravitational potential energy of a particle of mass \(m\) increases by \(mgh,\) when it is raised through a height \(h\) in a uniform gravitational field "\(g\)". If a particle of mass \(m\) is raised through a height \(h\) in the earth's gravitational field (\(g\): the field on the earth's surface) and the increase in gravitational potential energy is \(U\), then:

1.	\(U > mgh\)
2.	\(U < mgh\)
3.	\(U = mgh\)
4.	any of the above may be true depending on the value of \(h,\) considered relative to the radius of the earth.

Add Note

Subtopic: Gravitational Potential Energy |

From NCERT

Other Reason

Highlight in NCERT

Select Color:

Add Note (Optional):

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Upgrade Your Plan

Upgrade now and unlock your full question bank experience with daily practice.

Q10:

Two particles of masses \(m_1,~m_2\)are placed on the axis of a uniform circular ring of mass \(M\) and radius \(R,\) on opposite sides of the centre of the ring. The distances of \(m_1,~m_2\)from the centre of the ring are \(x_1,~x_2\) respectively, and \(x_1~ x_2 \ll R.\) The net force on the ring vanishes. Then,

1.	\(\dfrac{m_{1}}{x_{1}}=\dfrac{m_{2}}{x_{2}} \)	2.	\(\dfrac{m_{1}}{x_{1}^{2}}=\dfrac{m_{2}}{x_{2}^{2}} \)
3.	\(\dfrac{m_{1}}{x_{1}^{3}}=\dfrac{m_{2}}{x_{2}^{3}} \)	4.	\(m_{1} x_{1}=m_{2} x_{2} \)