+91-8527521718
Signup | Login
  • 1(current)
  • 2
Q. No.

Two rods of identical dimensions are joined end-to-end, and the ends of the composite rod are kept at \(0^\circ\text{C}\) and \(100^\circ\text{C}\) (as shown in the diagram). The temperature of the joint is found to be \(40^\circ\text{C}.\) Assuming no loss of heat through the sides of the rods, the ratio of the conductivities of the rods \(\dfrac{K_1}{K_2}\) is:

1. \(\dfrac32\) 2. \(\dfrac23\)
3. \(\dfrac11\) 4. \(\dfrac{\sqrt3}{\sqrt2}\)
Subtopic:  Conduction |
 80%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

If the ends of the meter stick are maintained at \(\theta_1\)\(^\circ \text{C}\) and \(\theta_2\)\(^\circ \text{C},\) the temperatures measured at the \(25\) cm and \(80\) cm marks are observed to be \(35^\circ \text{C}\) and \(68^\circ \text{C}\) respectively. Then the temperatures of the left end
(\(\theta_1\)\(^\circ \text{C}\)) and the right end (\(\theta_2\)\(^\circ \text{C}\)) are: 
1. \(\theta_{1}=0, ~\theta_{2}=90\)   
2. \(\theta_{1}=10,~\theta_{2}=85\)
3. \(\theta_{1}=20, ~\theta_{2}=80\)
4. \(\theta_{1}=30, ~\theta_{2}=100\)
Subtopic:  Conduction |
 70%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Uniform rods with the same lengths & cross-sections are connected end-to-end between two bodies which are maintained at \(0^\circ\text C\) & \(100^\circ\text C,\) as shown in the figure. Heat flows through the rods from the hotter body to the colder body; there being no loss through the sides of the rods. The conductivity of the rods are indicated as multiples of \(K.\) \(\theta\) indicates, in each case, the steady-state temperature at a junction (in Column I). The value of \(\theta\) is indicated in Column II, but these are in a different order. Match them.
Column I Column II
(A) (I) \(20^\circ\text C\)
(B) (II) \(40^\circ\text C\)
(C) (III) \(60^\circ\text C\)
(D) (IV) \(80^\circ\text C\)
 
1. \(\mathrm{A\text- II,B\text- III,C\text- II,D\text- IV}\)
2. \(\mathrm{A\text- III,B\text- II,C\text- II,D\text- IV}\)
3. \(\mathrm{A\text-III,B\text- II,C\text- IV,D\text- II}\)
4. \(\mathrm{A\text-II ,B\text- III,C\text- III,D\text- IV}\)
Subtopic:  Conduction |
 85%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
Two bodies \(A,B\) are maintained at temperatures \(\theta_A=100^\circ\text C\) and \(\theta_B=0^\circ\text C.\) Two thermally conducting rods \((P,~Q)\) of different conductivities and of different dimensions are connected between \(A\) and \(B.\) The conductivity of \(P\) is twice that of \(Q.\) The sides of the rods are insulated. If the mid-points of the two rods are connected to each other by a thin conducting wire (after equilibrium is reached),
1. heat would flow from \(P\) to \(Q\).
2. heat would flow from \(Q\) to \(P\).
3. no flow of heat occurs between \(P\) & \(Q\).
4. flow of heat may occur back and forth between \(P\) & \(Q,\) varying with time.
Subtopic:  Conduction |
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Four identical-sized insulated rods are connected as shown in the figure, making thermal contact at their ends. The junctions \(A,B\) are maintained at temperatures of \(100^\circ\text C\) & \(0^\circ\text C,\) respectively. The conductivities of the rods are \(K_1,K_2,K_3\) & \(K_4\) respectively. It is observed that the temperatures of junctions \(C,D\) are equal. Then, it can be concluded that:

1. \(K_1=K_2\) & \(K_3=K_4\)
2. \(K_1=K_2=K_3=K_4\)
3. \(K_1K_4=K_2K_3\)
4. \(K_1K_3=K_2K_4\)
Subtopic:  Conduction |
 74%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Three rods of identical dimensions but made of materials of conductivities \(K,~2K,~K\) are connected in series. The two ends \(A~,B\) are maintained at temperatures of \(0^{\circ} \text{C},~100^{\circ} \text{C}\) respectively. Assume no loss of heat from the sides. The temperatures of the junctions \(X,~Y\) are:
                  
1. \(25^\circ\text C,~75^\circ\text C\)
2. \(40^\circ\text C,~60^\circ\text C\)
3. \(20^\circ\text C,~80^\circ\text C\)
4. \(30^\circ\text C,~70^\circ\text C\)
Subtopic:  Conduction |
 70%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
Given below are two statements: 
Assertion (A): Thermal conduction occurs only in the presence of a temperature gradient.
Reason (R): In the absence of a temperature gradient (i.e., no temperature difference in space), thermal energy – which is transferred due to molecular (or particle) collisions, cannot be transferred in any particular direction.
 
1. Both (A) and (R) are True and (R) is the correct explanation of (A).
2. Both (A) and (R) are True but (R) is not the correct explanation of (A).
3. (A) is True but (R) is False.
4. (A) is False but (R) is True.
Subtopic:  Conduction |
 88%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

A cylindrical rod of copper \((AB)\) is insulated on its sides, and its two ends are kept at temperatures of \(100^\circ\text C\) (at \(A\)) and \(0^\circ\text C\) (at \(B\)). After sufficient time, the temperature at the mid-point of the rod becomes:
    
1. \(50^\circ\text C\)
2. \(100^\circ\text C\)
3. \(0^\circ\text C\)
4. any value between \(0^\circ\text C\) and \(100^\circ\text C,\) depending on its cross-section
Subtopic:  Conduction |
 62%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

If two rods, of identical dimensions but made of materials with conductivity \(K_1\) and \(K_2,\) are placed end-to-end, the combination behaves as a single rod of (average) conductivity \(K.\) Then, \(K\) satisfies:
      
1. \(K=K_1+K_2\)     2. \(K=\dfrac{K_1+K_2}{2}\)    
3. \(\dfrac{1}{K}=\dfrac{1}{K_1}+\dfrac{1}{K_2}\) 4. \(\Large\frac{2}{K}=\frac{1}{K_1}+\frac{1}{K_2}\)
Subtopic:  Conduction |
 57%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
Three rods of identical dimensions but made of different materials \(A,B\) are connected end-to-end, as shown in the figure. The left-most end is kept at \(100^\circ\text C\) while the right-most end is kept at \(0^\circ\text C.\) The conductivity of \(B\) is twice that of \(A;-\) the system is insulated on the sides and allowed to reach the steady state. The temperatures at junctions \(1\) and \(2\) (see figure) are:
            
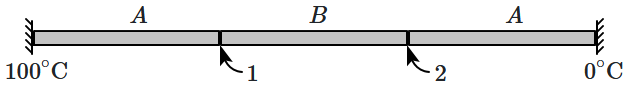
1. \(75^\circ\text C,~25^\circ\text C\)
2. \(60^\circ\text C,~40^\circ\text C\)
3. \(50^\circ\text C,~25^\circ\text C\)
4. \(80^\circ\text C,~40^\circ\text C\)
Subtopic:  Conduction |
 64%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

  • 1(current)
  • 2
Q. No.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions

© 2025 GoodEd Technologies Pvt. Ltd.