A particle moves from a point \(\left(\right. - 2 \hat{i} + 5 \hat{j} \left.\right)\) to \(\left(\right. 4 \hat{j} + 3 \hat{k} \left.\right)\) when a force of \(\left(\right. 4 \hat{i} + 3 \hat{j} \left.\right)\) \(\text{N}\) is applied. How much work has been done by the force?
1.
\(8\) J
2.
\(11\) J
3.
\(5\) J
4.
\(2\) J
In the given figure
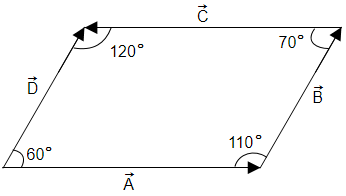
| 1. | Angle between \(\overrightarrow {A}\) and \(\overrightarrow {B}\) is \(110^{\circ}\) |
| 2. | Angle between \(\overrightarrow {C}\) and \(\overrightarrow {D}\) is \(60^{\circ}\) |
| 3. | Angle between \(\overrightarrow {B}\) and \(\overrightarrow {C}\) is \(110^{\circ}\) |
| 4. | Angle between \(\overrightarrow {B}\) and \(\overrightarrow {C}\) is \(70^{\circ}\) |
A force of 6 N and another of 8 N can be applied together to produce the effect of a single force of -
(1) 1 N
(2) 11 N
(3) 15 N
(4) 20 N
Which of the sets given below may represent the magnitude of resultant of three vectors adding to zero?
(1) 2, 4, 8
(2) 4, 8, 16
(3) 1, 2, 1
(4) 0.5, 1, 2
A blind person after walking 10 steps in one direction, each of length 80 cm, turns randomly to the left or to the right by After walking a total of 40 steps the maximum possible displacement of the person from his starting position could be -
(1)
(2)
(3)
(4)
The resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -
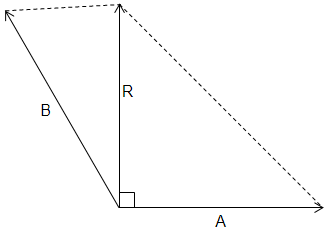
1.
2.
3.
4. None of these
The three vectors OA, OB and OC have the same magnitude R. Then the sum of these vectors have magnitude -
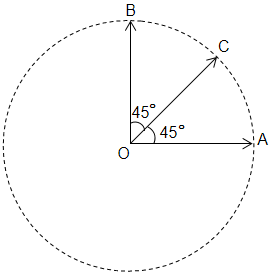
1.
2.
3.
4.
A truck travelling due north with 20m/s turns towards west and travels at the same speed. Then the change in velocity is -
(1) 40 m/s north-west
(2) m/s north-west
(3) 40 m/s south-west
(4) m/s south-west
A particle is moving in a circle of radius r centered at O with constant speed v. The change in velocity moving from A to B is -
(A)
(B)
(C)
(D)
What is the resultant of three coplanar forces: at , at and at ?
1.
2.
3.
4.




