Q. No.A spring of force constant \(k\) is cut into lengths of ratio \(1:2:3\). They are connected in series and the new force constant is \(k'\). Then they are connected in parallel and the force constant is \(k''\). Then \(k':k''\) is:
1. \(1:9\)
2. \(1:11\)
3. \(1:14\)
4. \(1:6\)
1. \(1:9\)
2. \(1:11\)
3. \(1:14\)
4. \(1:6\)
A pendulum is hung from the roof of a sufficiently high building and is moving freely to and fro like a simple harmonic oscillator. The acceleration of the bob of the pendulum is 20 m/s2 at a distance of 5 m from the mean position. The time period of oscillation is:
| 1. | 2 s | 2. | s |
| 3. | 2 s | 4. | 1 s |
A particle is executing a simple harmonic motion. Its maximum acceleration is and maximum velocity is . Then its time period of vibration will be:
| 1. | \(\frac {\beta^2}{\alpha^2}\) | 2. | \(\frac {\beta}{\alpha}\) |
| 3. | \(\frac {\beta^2}{\alpha}\) | 4. | \(\frac {2\pi \beta}{\alpha}\) |
A particle is executing SHM along a straight line. Its velocities at distances \(x_1\) and \(x_2\) from the mean position are \(v_1\) and \(v_2\), respectively. Its time period is:
| 1. | \(2 \pi \sqrt{\dfrac{x_{1}^{2}+x_{2}^{2}}{v_{1}^{2}+v_{2}^{2}}}~\) | 2. | \(2 \pi \sqrt{\dfrac{{x}_{2}^{2}-{x}_{1}^{2}}{{v}_{1}^{2}-{v}_{2}^{2}}}\) |
| 3. | \(2 \pi \sqrt{\dfrac{v_{1}^{2}+v_{2}^{2}}{x_{1}^{2}+x_{2}^{2}}}\) | 4. | \(2 \pi \sqrt{\dfrac{v_{1}^{2}-v_{2}^{2}}{x_{1}^{2}-x_{2}^{2}}}\) |
The oscillation of a body on a smooth horizontal surface is represented by the equation, \(X=A \text{cos}(\omega t)\),
where \(X=\) displacement at time \(t,\) \(\omega=\) frequency of oscillation.
Which one of the following graphs correctly shows the variation of acceleration, \(a\) with time, \(t?\)
(\(T=\) time period) \(a~~O~~T~~t~~\)
| 1. |  |
2. |  |
| 3. |  |
4. |  |
1. Only (IV) does not represent SHM
2. (I) and (III)
3. (I) and (II)
4. Only (I)
A particle of mass \(m\) is released from rest and follows a parabolic path as shown. Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time?
| 1. |  |
2. |  |
| 3. |  |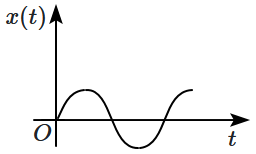
4. |  |
1. \(\frac{\pi a\sqrt3}{2T}\)
2. \(\frac{\pi a}{T}\)
3. \(\frac{3\pi^2 a}{T}\)
4. \(\frac{\pi a\sqrt3}{T}\)
1. Acceleration = -k0x + k1x2
2. Acceleration = -k(x+a)
3. Acceleration = k(x+a)
4. Acceleration = kx
1. 1: 10
2. 1: 102
3. 1: 103
4. 1: 104
© 2024 GoodEd Technologies Pvt. Ltd.