Light enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face what so ever be the value of angle of incidence
(1)
(2)
(3)
(4)
One face of a rectangular glass plate 6 cm thick is silvered. An object held 8 cm in front of the first face, forms an image 10 cm behind the silvered face. The refractive index of the glass is [Consider that light ray returns back in the first medium]
(1) 0.4
(2) 0.8
(3) 1.5
(4) 1.6
Two transparent slabs have the same thickness as shown. One is made of material A of refractive index 1.5. The other is made of two materials B and C with thickness in the ratio 1:2. The refractive index of C is 1.6. If a monochromatic parallel beam passing through the slabs has the same number of waves inside both, the refractive index of B is
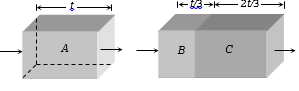

1. 1.1
2. 1.2
3. 1.3
4. 1.4
The image of point P when viewed from the top of the slabs will be
(1) 2.0 cm above P
(2) 1.5 cm above P
(3) 2.0 cm below P
(4) 1 cm above P
| 1. | \(6\) cm | 2. | \(9\) cm |
| 3. | \(12\) cm | 4. | \(15\) cm |
1. \(2R\)
2. \(R\)
3. \(\frac{3}{2}R\)
4. \(R^2\)
A prism having an apex angle \(4^{\circ}\) and refraction index \(1.5\) is located in front of a vertical plane mirror as shown in the figure. Through what total angle is the ray deviated after reflection from the mirror?
1. \(176^{\circ}\)
2. \(4^{\circ}\)
3. \(178^{\circ}\)
4. \(2^{\circ}\)
A rectangular glass slab ABCD, of refractive index , is immersed in water of the refractive index . A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence , such that the ray comes out only from the other surface CD is given by
1.
2.
3.
4.
A rod of glass \((\mu = 1.5)\) and of the square cross-section is bent into the shape as shown. A parallel beam of light falls on the plane's flat surface \(A\) as shown in the figure. If \(d\) is the width of a side and \(R\) is the radius of a circular arc then for what maximum value of \(\frac{d}{R},\) light entering the glass slab through surface \(A\) will emerge from the glass through \(B?\)

| 1. | \(1.5\) | 2. | \(0.5\) |
| 3. | \(1.3\) | 4. | None of these |
A diverging beam of light from a point source \(S\) having divergence angle \(\alpha,\) falls symmetrically on a glass slab as shown. The angles of incidence of the two extreme rays are equal. If the thickness of the glass slab is \(t\) and the refractive index \(n\), then the divergence angle of the emergent beam is:
| 1. | zero | 2. | \(\alpha\) |
| 3. | \(\sin^{-1}\left(\frac{1}{n}\right)\) | 4. | \(2\sin^{-1}\left(\frac{1}{n}\right)\) |






