A particle is moving three times as fast as an electron. The ratio of the de Broglie wavelength of the particle to that of the electron is . The particle’s mass is:
What is the de Broglie wavelength associated with an electron, accelerated through a potential difference of \(100\) V?
1. \(0.123\) nm
2. \(0.232\) nm
3. \(0.031\) nm
4. \(0.312\) nm
Graph shows variation of photoelectric current with intensity of light. It can be concluded that photoelectrons emitted per second are-
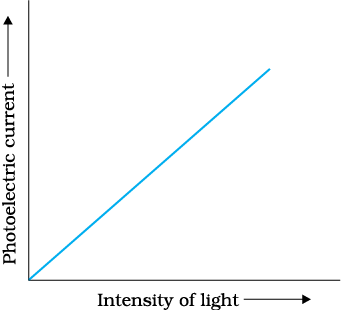
1. Independent of intensity of incident radiation
2. Inversely proportional to intensity of incident radiation
3. Directly proportional to intensity of incident radiation
4. Directly proportional to square of intensity of incident radiation
The graph shows the variation of photocurrent with collector plate potential for different intensities of incident radiation. Then the maximum intensity is:
1.
2.
3.
4. All intensities are same
The wavelength of light in the visible region is about \(550\) nm (average wavelength) for yellow-green colour. Three materials with work functions are given as Al (\(4.28\) eV), Cu (\(4.65\) eV) and Na (\(2.75\) eV). From which of these photosensitive materials, can you build a photoelectric device that operates with visible light?
1. Al
2. Cu
3. Na
4. none of the above
The number of photons per second on an average emitted by a source of monochromatic light of wavelength \(600~\text{nm}\), when it delivers the power of \(3.3\times 10^{-3}\) watt will be:
\((h = 6.6\times10^{-34}~\text{J-s})\)
| 1. | \(10^{16}\) | 2. | \(10^{15}\) |
| 3. | \(10^{18}\) | 4. | \(10^{17}\) |
An electromagnetic wave of wavelength \(\lambda\) is incident on a photosensitive surface of negligible work function. If '\(m\)' is the mass of photoelectron emitted from the surface and \(\lambda_d\) is the de-Broglie wavelength, then:
1. \( \lambda=\left(\frac{2 {mc}}{{h}}\right) \lambda_{{d}}^2 \)
2. \( \lambda=\left(\frac{2 {h}}{{mc}}\right) \lambda_{{d}}^2 \)
3. \( \lambda=\left(\frac{2 {m}}{{hc}}\right) \lambda_{{d}}^2\)
4. \( \lambda_{{d}}=\left(\frac{2 {mc}}{{h}}\right) \lambda^2 \)
An electron, an \(α\text-\)particle, and a proton have the same kinetic energy. Which of these particles has the shortest de Broglie wavelength?
1. Electron
2. \(α\text-\)particle
3. Proton
4. All have the same de Broglie wavelength
The de-Broglie wavelength associated with a ball of mass \(150~\text{g}\) travelling at a speed of \(30.0~\text{m/s}\) is:
1. \(1.47\times10^{-32}~\text{m}\)
2. \(2.01\times10^{-34}~\text{m}\)
3. \(2.01\times10^{-32}~\text{m}\)
4. \(1.47\times10^{-34}~\text{m}\)
What is the de-Broglie wavelength associated with an electron moving at a speed of \(5.4\times10^6~\text{m/s}\)?
| 1. | \(0.244~\text{nm}\) | 2. | \(0.135~\text{nm}\) |
| 3. | \(0.157~\text{nm}\) | 4. | \(0.111~\text{nm}\) |







