A body oscillates with SHM according to the equation (in SI units), \(x= 5\cos\left[2\pi t +\frac{\pi}{4}\right].\) At \(t = 1.5\) s, acceleration of the body will be:
1.
\(140 \text{ cm} / \text{s}^2 \)
2.
\(160 \text{ m} / \text{s}^2 \)
3.
\(140 \text{ m} / \text{s}^2 \)
4.
\(14 \text{ m} / \text{s}^2\)
A block is fastened to a spring. The spring has a spring constant of \(50\) N m–1. The block is pulled to a distance \(x = 10\) cm from its equilibrium position at \(x =0\) on a frictionless surface from rest at \(t=0.\) The potential and total energies of the block when it is \(5\) cm away from the mean position respectively are:
| 1. | \(0.0625\) J and \(0.25 \) J | 2. | \(0.625\) J and \(0.25\) J |
| 3. | \(0.0325\) J and \(0.35\) J | 4. | \(0.065\) J and \(3.5 \) J |
For the damped oscillator shown in the figure, the mass m of the block is \(200\) g, \(k=90\) N/m and the damping constant \(b\) is \(40\) g/s. The time taken for its amplitude of vibrations to drop to half of its initial value is:
1. \(5.93\) s
2. \(6.93\) s
3. \(7.93\) s
4. \(0.3\) s
For the damped oscillator shown in the figure, the mass m of the block is 200 g, k = 90 N/m and the damping constant b is 40 g/s. The time taken for its mechanical energy to drop to half its initial value is:
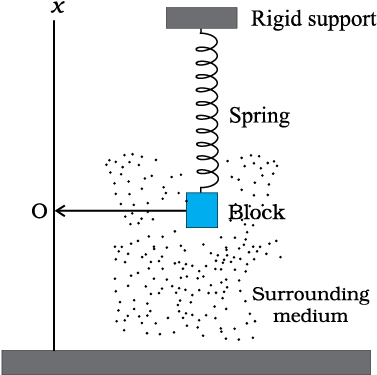
1. 3.46 s
2. 4.36 s
3. 6.93 s
4. 0.3 s
The graph shows displacement versus time graph for a particle performing SHM along x-axis given by . Value of the initial phase, of the particle is-
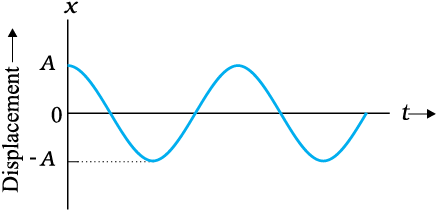
1.
2.
3.
4.
The given graph shows displacement versus time graph for a particle performing Simple Harmonic Motion (SHM) for two values of the initial phase .
The correct equation for the SHM that can be deduced from the above graph is:
The figure given below shows the graphs for amplitudes of forced oscillations in resonance conditions for different damping conditions.
One of the conclusions that can be drawn from the graph above is:
1. As damping increases, amplitude increases
2. As damping increases, the amplitude decreases
3. As damping increases, the amplitude does not change
4. As damping increases, the amplitude may increase or decrease
| 1. | \(3n\) | 2. | \(4n\) |
| 3. | \(n\) | 4. | \(2n\) |
A spring is stretched by \(5~\text{cm}\) by a force \(10~\text{N}\). The time period of the oscillations when a mass of \(2~\text{kg}\) is suspended by it is:
1. \(3.14~\text{s}\)
2. \(0.628~\text{s}\)
3. \(0.0628~\text{s}\)
4. \(6.28~\text{s}\)
Which of the following statements is/are correct.
| a. | Motion of a kink in a longitudinal spring produced by displacing one end of the spring sideways is transverse and longitudinal, both. |
| b. | Waves produced in a cylinder containing a liquid by moving its piston back and forth is longitudinal. |
| c. | Waves produced by a motorboat sailing in water are transverse and longitudinal, both. |
| d. | Ultrasonic waves in air produced by a vibrating quartz crystal are longitudinal. |
1. (a), (b) and (d)
2. (b) and (d)
3. (a), (c) and (d)
4. All are correct









