The polarity of the capacitor in the given figure is:

     

1.	The polarity of plate ‘\(B\)’ will be positive with respect to plate ‘\(A.\)’
2.	The polarity of plate ‘\(A\)’ will be positive with respect to plate ‘\(B.\)’
3.	The polarity of plate ‘\(A\)’ will be the same as that of plate ‘\(B.\)’
4.	None of these

 

A metallic rod of \(1 ~\text m\) length is rotated with a frequency of \(50 ~\text{rev/s},\) with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius \(1 ~\text m,\) about an axis passing through the centre and perpendicular to the plane of the ring (as shown in the figure). A constant and uniform magnetic field of \(1 ~\text T\) parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?

   
1. \(150 ~\text V\)
2. \(130 ~\text V\)
3. \(157 ~\text V\)
4. \(133 ~\text V\)

A wheel with \(10\) metallic spokes each \(0.5\) m long is rotated with a speed of \(120\) rev/min in a plane normal to the horizontal component of earth’s magnetic field H_E at a place. If \(H_E=0.4\) G at the place, what is the induced emf between the axle and the rim of the wheel? (\(1\) G=\(10^{-4}\) T)
1. \(5.12\times10^{-5}\) T
2. \(0\)
3. \(3.33\times10^{-5}\)
4. \(6.28\times10^{-5}\)

Refer to figure. The arm \(PQ\) of the rectangular conductor is moved from \(x = 0,\) outwards. The uniform magnetic field is perpendicular to the plane and extends from \(x = 0\) to \(x = b\) and is zero for \(x > b.\) Only the arm \(PQ\) possesses substantial resistance \(r.\) Consider the situation when the arm \(PQ\) is pulled outwards from \(x = 0\) to \(x = 2b\) with a` constant speed \(v.\) The induced emf is:

$\mathrm{}$
$\mathrm{}$
1. \(- Blv   ~\text{for }~  0 \leq x < b ,~~~   0   ~\text{for}~   b \leq x < 2 b\)
2. \(  + Blv   ~\text{for}~   0 \leq x < b ,   ~~~0   ~\text{for }~  b \leq x < 2 b\)
3. \(- Blv   ~\text{for}~   b \leq x < 2 b ,  ~~~0 ~\text{for }~  0 \leq x < b\)
4. \(+ Blv  ~\text{for}  ~ b \leq x < 2 b , ~~~  0  ~\text{for}~   0 \leq x < b\)
$$

$\mathrm{}$

Refer to the figure. The arm PQ of the rectangular conductor is moved from x = 0, outwards. The uniform magnetic field is perpendicular to the plane and extends from x = 0 to x = b and is zero for x > b. Only the arm PQ possesses substantial resistance r. Consider the situation when the arm PQ is pulled outwards from x = 0 to x = 2b with constant speed v. The force necessary to pull the arm is:

$1. \frac{{\mathrm{B}}^2{\mathrm{l}}^2\mathrm{v}}{\mathrm{r}} \mathrm{for} 0\le \mathrm{x}<\mathrm{b}, 0 \mathrm{for} \mathrm{b}\le \mathrm{x}<2\mathrm{b}$
$2. \frac{{\mathrm{B}}^2{\mathrm{l}}^2\mathrm{v}}{2\mathrm{r}} \mathrm{for} 0\le \mathrm{x}<\mathrm{b}, 0 \mathrm{for} \mathrm{b}\le \mathrm{x}<2\mathrm{b}$
$3. 0 \mathrm{for} 0\le \mathrm{x}<\mathrm{b}, \frac{{\mathrm{B}}^2{\mathrm{l}}^2\mathrm{v}}{\mathrm{r}} \mathrm{for} \mathrm{b}\le \mathrm{x}<2\mathrm{b}$
$4. 0 \mathrm{for} 0\le \mathrm{x}<\mathrm{b}, \frac{{\mathrm{B}}^2{\mathrm{l}}^2\mathrm{v}}{2\mathrm{r}} \mathrm{for} \mathrm{b}\le \mathrm{x}<2\mathrm{b}$

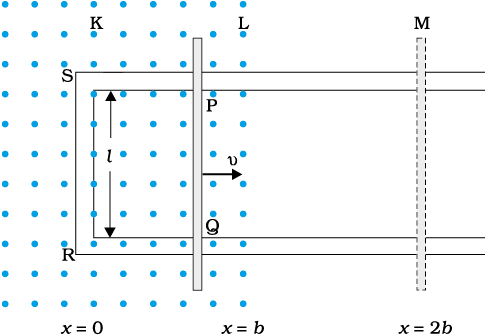
The arm \(PQ\) of the rectangular conductor is moved from \(x = 0,\) outwards. The uniform magnetic field is perpendicular to the plane and extends from \(x = 0\) to \(x = b\) and is zero for \(x > b.\) Only the arm \(PQ\) possesses substantial resistance \(r.\) Consider the situation when the arm \(PQ\) is pulled outwards from \(x = 0\) to \(x = 2b\) and is then moved back to \(x = 0\) with constant speed \(v.\) The power dissipated as Joule heat is: 

                
1. \(\dfrac{{B}^2 {l}^2 {v}}{2{r}}~~\text{for}~0 \leq {x}<{b},~~~ 0~~\text{for} ~{b} \leq {x}<2 {b}\)

2. \(\dfrac{{B}^2 {l}^2 {v^2}}{{r}}~~\text{for}~0 \leq {x}<{b},~~~ 0~~\text{for} ~{b} \leq {x}<2 {b}\)

3. \(0~~\text{for}~b \leq {x}<{2b},~~~ \dfrac{{B}^2 {l}^2 {v}^2}{{r}}~~\text{for} ~{0} \leq {x}< {b}\)

4. \(0~~\text{for}~b \leq {x}<{2b},~~~ \dfrac{{B}^2 {l}^2 {v}}{{2r}}~~\text{for} ~{0} \leq {x}< {b}\)

Two concentric circular coils, one of small radius \({r_1}\) and the other of large radius \({r_2},\) such that \({r_1<<r_2},\)  are placed co-axially with centres coinciding. The mutual inductance of the arrangement is:
1. \(\dfrac{\mu_0\pi r_1^2}{3r_2}\)
2. \(\dfrac{2\mu_0\pi r_1^2}{r_2}\)
3. \(\dfrac{\mu_0\pi r_1^2}{r_2}\)
4. \(\dfrac{\mu_0\pi r_1^2}{2r_2}\)

The expression for the magnetic energy stored in a solenoid in terms of magnetic field \(B\), area \(A\) and length \(l\) of the solenoid is:

The ratio of magnetic energy per unit volume and electrostatic energy stored per unit volume in a parallel plate capacitor is:
1. \(\left(\dfrac{1}{\varepsilon_0 \mu_0}\right)\dfrac{B^2}{E}\)

2. \(\left(\dfrac{1}{\varepsilon_0 \mu_0}\right)\dfrac{E^2}{B}\)

3. \(\left(\dfrac{1}{2\varepsilon_0 \mu_0}\right)\dfrac{B^2}{E}\)

4. \(\left(\dfrac{1}{2\varepsilon_0 \mu_0}\right)\dfrac{E^2}{B}\)$\mathrm{}$

Kamla peddles a stationary bicycle. The pedals of the bicycle are attached to a \(100\) turn coil of an area of \(0.10~\text{m}^2\). The coil rotates at half a revolution per second and it is placed in a uniform magnetic field of \(0.01~\text{T}\) perpendicular to the axis of rotation of the coil. What is the maximum voltage generated in the coil?
1. \(0.628~\text{V}\)
2. \(0.421~\text{V}\)
3. \(0.314~\text{V}\)
4. \(0\)