A blacksmith fixes an iron ring on the rim of the wooden wheel of a horse cart. The diameter of the rim and the iron ring are \(5.012\) m and \(5.00\) m, respectively at \(27^{\circ}\text{C}.\) To what temperature should the ring be heated so as to fit the rim of the wheel?
\(\left(\text{Given:}~\alpha~\text{for iron}= 1.20 \times 10^{-5}~^\circ{\text{C}^{-1}}\right)\)
1. \(128^{\circ}\text{C}\)
2. \(118^{\circ}\text{C}\)
3. \(227^{\circ}\text{C}\)
4. \(218^{\circ}\text{C}\)
\(\left(\text{Given:}~\alpha~\text{for iron}= 1.20 \times 10^{-5}~^\circ{\text{C}^{-1}}\right)\)
1. \(128^{\circ}\text{C}\)
2. \(118^{\circ}\text{C}\)
3. \(227^{\circ}\text{C}\)
4. \(218^{\circ}\text{C}\)
A sphere of \(0.047\) kg aluminium is placed for sufficient time in a vessel containing boiling water so that the sphere is at \(100^{\circ}\text{C}\). It is then immediately transferred to a \(0.14\) kg copper calorimeter containing \(0.25\) kg water at \(20^{\circ}\text{C}\). The temperature of water rises and attains a steady-state at \(23^{\circ}\text{C}\). The specific heat capacity of aluminium is:
(Given that: Specific heat capacity of copper calorimeter \(= 0.386\times 10^{3}~\text{J kg}^{-1}\text{K}^{-1}\) and the specific heat capacity of water \(s_w= 4.18\times 10^{3}~\text{J kg}^{-1}\text{K}^{-1})\)
1. \(1.811~\text{kJ kg}^{-1}\text{K}^{-1}\)
2. \(1.911~\text{kJ kg}^{-1}\text{K}^{-1}\)
3. \(0.811~\text{kJ kg}^{-1}\text{K}^{-1}\)
4. \(0.911~\text{kJ kg}^{-1}\text{K}^{-1}\)
When \(0.15\) kg of ice at \(0^\circ \text{C}\) is mixed with \(0.30\) kg of water at \(50^\circ \text{C}\) in a container, the resulting temperature is \(6.7^\circ \text{C}.\)
The heat of fusion of ice is: (\(S_{\text{water}}=4186\) J kg–1 K–1)
1. \( 3.43 \times 10^4\) Jkg–1
2. \( 3.34 \times 10^4\) Jkg–1
3. \( 3.34 \times 10^5\) Jkg–1
4. \(4.34 \times 10^5\) Jkg–1
(given, the specific heat capacity of \(\text{ice}= 2100~\text{J kg}^{-1}\text{K}^{-1},\) the specific heat capacity of \(\text{water}= 4186~\text{J kg}^{-1}\text{K}^{-1},\) the latent heat of fusion of \(\text{ice}= 3.35\times 10^{5}~\text{J kg}^{-1}\) and the latent heat of \(\text{steam}= 2.256\times 10^6~\text{J kg}^{-1}\))
| 1. | \(9.1\times 10^{7}~\text{J}\) | 2. | \(8.1\times 10^{6}~\text{J}\) |
| 3. | \(9.1\times 10^{6}~\text{J}\) | 4. | \(8.1\times 10^{7}~\text{J}\) |
What is the temperature of the steel-copper junction in the steady-state of the system shown in the figure? The length of the steel rod = \(15.0\) cm, length of the copper rod = \(10.0\) cm, temperature of the furnace = \(300^{\circ}\text{C}\), temperature of the other end = \(0^{\circ}\text{C}\). The area of the cross section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel = \(50.2 ~\text{J s}^{-1}\text{m}^{-1}\text{K}^{-1};\) and of copper \(= 385~\text{J s}^{-1}\text{m}^{-1}\text{K}^{-1})\).
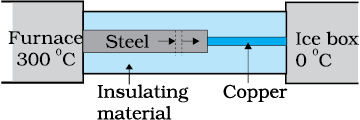
1. \(44.4^{\circ}\text{C}\)
2. \(44.4~\text{K}\)
3. \(54.4^{\circ}\text{C}\)
4. \(54.4~\text{K}\)
An iron bar
\(\left(L_{1}=0.1 \text{m} , A_{1}=0.02~\text{m}^{2} , K_{1}=79~\text{Wm}^{- 1} \text{K}^{-1}\right)\) and a brass bar
\(\left(L_{2}=0.1~\text{m} , A_{2}=0.02~\text{m}^{2} , K_{2}=109~\text{Wm}^{- 1} \text{K}^{- 1}\right)\) are soldered end to end as shown in the figure. The free ends of the iron bar and brass bar are maintained at \(373~ \text{K}\) and \(273~ \text{K}\) respectively. The temperature of the junction of the two bars is:

1. \(215~ \text{K}\)
2. \(315~ \text{K}\)
3. \(415~ \text{K}\)
4. \(115~ \text{K}\)
1. \(50\) s
2. \(52\) s
3. \(42\) s
4. \(48\) s
An iron bar \(K_1 = 79~\text{W m}^{-1}\text{K}^{-1}\) and a brass bar \(K_2 = 109~\text{W m}^{-1}\text{K}^{-1}\) are soldered end to end as shown in the figure. The free ends of the iron bar and brass bar are maintained at \(373\) K and \(273\) K respectively. Then the equivalent thermal conductivity of the compound bar is:

| 1. | \(94.6~\text{W m}^{-1}\text{K}^{-1}\) | 2. | \(93.6~\text{W m}^{-1}\text{K}^{-1}\) |
| 3. | \(81.6~\text{W m}^{-1}\text{K}^{-1}\) | 4. | \(91.6~\text{W m}^{-1}\text{K}^{-1}\) |
An iron bar \(\left(L_{1} = 0 . 1 ~ \text{m}, A_{1} = 0 . 02 ~\text{m}^{2}, K_{1} = 79~\text{W m}^{- 1} \text{K}^{- 1}\right)\) and a brass bar \(\left(L_{2}= 0 . 1 ~\text{m}, A_2 = 0.02~\text{m}^2, K_2 = 109~\text{W m}^{-1}\text{K}^{-1}\right)\) are soldered end to end as shown in the figure. The free ends of the iron bar and brass bar are maintained at \(373\) K and \(273\) K respectively. The heat current through the compound bar is:

1. \(916.1\) W
2. \(826.1\) W
3. \(926.1\) W
4. \(726\) W
The given graph shows the variation of Fahrenheit temperature () vs Celsius temperature (). The correct relation between the two temperature scales that can be deduced from the graph below is







