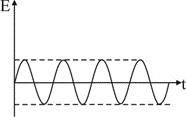
Which of the diagrams represents variation of the total mechanical energy of a pendulum oscillating in air as a function of time?
1. 
2. 
3. 
4. 




The rotation of the earth about its axis is:
| 1. | periodic motion |
| 2. | simple harmonic motion |
| 3. | periodic and simple harmonic motion |
| 4. | non-periodic motion |
The displacement of a particle is represented by the equation \(y= 3 \cos \left(\frac{\pi}{4}-\omega t \right)\). The motion of the particle is:
| 1. | simple harmonic with period \(\dfrac{2\pi}{\omega}\) |
| 2. | simple harmonic with period \(\dfrac{\pi}{\omega}\) |
| 3. | periodic but not simple harmonic |
| 4. | non-periodic |
The displacement of a particle is represented by the equation; \(y =\sin^{3}\omega t.\) The motion is:
| 1. | non-periodic. |
| 2. | periodic but not simple harmonic. |
| 3. | simple harmonic with period \(2\pi / \omega.\) |
| 4. | simple harmonic with period \(\pi / \omega.\) |
The relations between acceleration and displacement of four particles are given below. Which one of the particles is executing simple harmonic motion?
| 1. | \(a_1 = +2x\) | 2. | \(a_1= +2x^2\) |
| 3. | \(a_1= -2x^2\) | 4. | \(a_1 = -2x\) |
A particle is acted simultaneously by mutually perpendicular simple harmonic motion \(x=a \text{cos}𝜔𝑡\) and \(y = a\text{sin} 𝜔 𝑡\). The trajectory of motion of the particle will be:
1. an ellipse
2. a parabola
3. a circle
4. a straight line
The displacement of a particle varies with time according to the relation, \(y=a~\text{sin} \omega t+b~\text{cos} \omega t.\)
| 1. | the motion is oscillatory but not SHM |
| 2. | the motion is SHM with amplitude \(a+b\) |
| 3. | the motion is SHM with amplitude \(a^{2}+b^{2}\) |
| 4. | the motion is SHM with amplitude \(\sqrt{a^{2}+b^{2}}\) |
Four pendulums \(A,B,C,\) and \(D\) are suspended from the same elastic support as shown in the figure. \(A\) and \(C\) are of the same length, while \(B\) is smaller than \(A\) and \(D\) is large than \(A.\) If \(A\) is given a transverse displacement,

| 1. | \(D\) will vibrate with maximum amplitude. |
| 2. | \(C\) will vibrate with maximum amplitude. |
| 3. | \(B\) will vibrate with maximum amplitude. |
| 4. | All four will oscillate with equal amplitude. |
The figure shows the circular motion of a particle. The radius of the circle, the period, the sense of revolution, and the initial position are indicated in the figure. The simple harmonic motion of the \({x\text-}\)projection of the radius vector of the rotating particle \(P\) will be:

1. \(x \left( t \right) = B\text{sin} \left(\dfrac{2 πt}{30}\right)\)
2. \(x \left( t \right) = B\text{cos} \left(\dfrac{πt}{15}\right)\)
3. \(x \left( t \right) = B\text{sin} \left(\dfrac{πt}{15} + \dfrac{\pi}{2}\right)\) \(\)
4. \(x \left( t \right) = B\text{cos} \left(\dfrac{πt}{15} + \dfrac{\pi}{2}\right)\)
The equation of motion of a particle is \(x =a \text{cos} ( \alpha t )^{2}\). The motion is:
1. periodic but not oscillatory
2. periodic and oscillatory
3. oscillatory but not periodic
4. neither periodic nor oscillatory






