An ideal gas with an adiabatic exponent is heated at a constant pressure. It absorbs Q amount of heat. The fraction of heat absorbed in increasing the temperature is:
1.
2.
3.
4.
By opening the door of a refrigerator inside a closed room:
1. you can cool the room to a certain degree.
2. you can cool it to the temperature inside the refrigerator.
3. you ultimately warm the room slightly.
4. you can neither cool nor warm the room.
In a Carnot cycle, order of process is:
1. isothermal expansion, adiabatic expansion, isothermal compression and adiabatic compression.
2. isothermal compression, isothermal expansion, adiabatic compression, and adiabatic expansion.
3. adiabatic expansion, isothermal compression , isothermal expansion, and adiabatic compression.
4. none of the above.
Consider a cycle followed by an engine, \(1~\text{to}~2\) is isothermal, \(2~\text{to}~3\) is adiabatic, \(3~\text{to}~1\) is adiabatic. Such a process does not exist because:
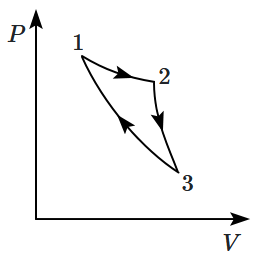
| 1. | heat is completely converted to mechanical energy in such a process |
| 2. | mechanical energy is completely converted to heat in this process, which is not possible. |
| 3. | curves representing two adiabatic processes don't intersect. |
| 4. | curves representing an adiabatic process and an iso-thermal process don't intersect. |
For a certain process, the pressure of a diatomic gas varies according to the relation , where a is a constant. What is the molar heat capacity of the gas for this process?
1.
2.
3.
4.
Work done in the cyclic process shown in the figure is:
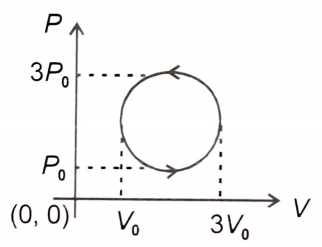
1.
2.
3.
4.
A certain amount of an ideal monatomic gas needs 20 J of heat energy to raise its temperature by at constant pressure. The heat needed for the same temperature rise at constant volume will be:
1. 30 J
2. 12 J
3. 200 J
4. 215.3 J
Select the incorrect statement about the specific heats of a gaseous system.
1. Specific heat at no exchange condition,
2. Specific heat at a constant temperature,
3. Specific heat at constant pressure,
4. Specific heat at constant volume,
(where symbols have their usual meanings)
1. \(C_P = \frac{\gamma R}{\gamma-1 }\)
2. \(C_P-C_V= R\)
3. \(\Delta U = \frac{P_fV_f-P_iV_i}{1-\gamma}\)
4. \(C_V = \frac{R}{\gamma-1 }\)
In the following figures (a) to (d), the variation of volume by change of pressure is shown. The gas is taken along the path ABCDA. The change in internal energy of the gas will be:
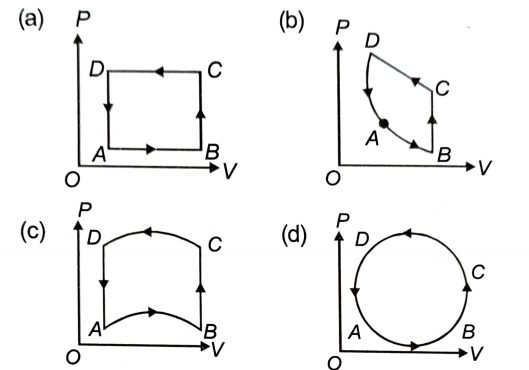
1. positive in all cases from (a) to (d).
2. positive in cases (a), (b) and (c) but zero in case (d).
3. negative in cases (a), (b) and (c) but zero in case (d).
4. zero in all four cases.






