A 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes?
(Assuming 50% of power is used up in heating the machine itself or lost to the surroundings? Specific heat of aluminium .)
1. 103°C
2. 109°C
3. 211°C
4. 197°C
(Assuming 50% of power is used up in heating the machine itself or lost to the surroundings? Specific heat of aluminium .)
1. 103°C
2. 109°C
3. 211°C
4. 197°C
In an experiment on the specific heat of a metal, a \(0.20~\text{kg}\) block of the metal at \(150^{\circ}\text{C}\) is dropped in a copper calorimeter (of water equivalent of \(0.025~\text{kg}\)) containing \(150~\text{cm}^{3}\) of water at \(27^{\circ}\text{C}.\) The final temperature is \(40^{\circ}\text{C}.\) The specific heat of the metal will be:
(the heat losses to the surroundings are negligible)
1. \(0 . 40 ~ \text{Jg}^{- 1} \text{K}^{- 1}\)
2. \(0 . 43 ~ \text{Jg}^{- 1} \text{K}^{- 1}\)
3. \(0 . 54 ~ \text{Jg}^{- 1} \text{K}^{- 1}\)
4. \(0 . 61 ~ \text{Jg}^{- 1} \text{K}^{- 1}\)
A copper block of mass 2.5 kg is heated in a furnace to a temperature of 500 °C and then placed on a large ice block. What is the maximum amount of ice that can melt?
(Specific heat of copper = the heat of fusion of water = 335 J/g)
1. 1.32 kg
2. 1.12 kg
3. 1.45 kg
4. 1.53 kg
Temperature is a measure of:
1. Hotness or coldness
2. Heat possessed by a body
3. Potential energy
4. Thermal energy
If in the winter season, the surface temperature of the lake is , the temperature at the bottom of the lake will be:
1.
2.
3.
4. All values less than are possible.
The readings of a bath on Celsius and Fahrenheit thermometers are in the ratio of 2: 5. The temperature of the bath is:
1.
2.
3.
4.
A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at . The diameter of the hole, when it is heated to 35.0 °C, is:
1. less than 4.24 cm.
2. equal to 4.24 cm.
3. more than 4.24 cm.
4. Data insufficient
On heating, a uniform metallic cylinder length increases by 3%. The area of cross-section of its base will increase by:
1. 1.5%
2. 3%
3. 9%
4. 6%
A circular metallic disc of radius R has a small circular cavity of radius r as shown in the figure. On heating the system,
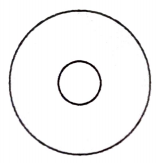
1. R increases and r decreases.
2. R decreases and r increases.
3. Both R and r increases.
4. Both R and r decreases.
A uniform copper rod of length 50 cm and diameter 3.0 mm is kept on a frictionless horizontal surface at 20 °C. The coefficient of linear expansion of copper is and Young's modulus is . The copper is heated to 100°C, then the tension developed in the copper rod is:
1.
2.
3.
4. Zero






