Select Question Set:
Q. No.In a uniform magnetic field of \(0.049~\text T\), a magnetic needle performs \(20\) complete oscillations in \(5\) seconds as shown. The moment of inertia of the needle is \(9.8 × 10^{-6} ~\text{kg m}^2\). If the magnitude of magnetic moment of the needle is \(x \times 10^{-5 }~\text {Am}^2;\) then the value of '\(x\)' is:
1. \(128\pi^2\)
2. \(50\pi^2\)
3. \(1280\pi^2\)
4. \(5\pi^2\)
1. \(128\pi^2\)
2. \(50\pi^2\)
3. \(1280\pi^2\)
4. \(5\pi^2\)
Subtopic: Bar Magnet |
From NCERT
NEET - 2024
Please attempt this question first.
Hints
Please attempt this question first.
Match List-I with List-II.
Choose the correct answer from the options given below:
1. \(\text{A-II, B-I, C-III, D-IV}\)
2. \(\text{A-III, B-II, C-I, D-IV}\)
3. \(\text{A-IV, B-III, C-II, D-I}\)
4. \(\text{A-II, B-III, C-IV, D-I}\)
| List-I (Material) |
List-II (Susceptibility (\(\chi\))) |
||
| \(\mathrm{A.}\) | Diamagnetic | \(\mathrm{I.}\) | \(\chi=0\) |
| \(\mathrm{B.}\) | Ferromagnetic | \(\mathrm{II.}\) | \(0>\chi\geq-1\) |
| \(\mathrm{C.}\) | Paramagnetic | \(\mathrm{III.}\) | \(\chi\gg1\) |
| \(\mathrm{D.}\) | Non-magnetic | \(\mathrm{IV.}\) | \(0<\chi<\varepsilon\) (a small positive number) |
1. \(\text{A-II, B-I, C-III, D-IV}\)
2. \(\text{A-III, B-II, C-I, D-IV}\)
3. \(\text{A-IV, B-III, C-II, D-I}\)
4. \(\text{A-II, B-III, C-IV, D-I}\)
Subtopic: Magnetic Materials |
63%
From NCERT
NEET - 2024
Please attempt this question first.
Hints
Please attempt this question first.
In the above diagram, a strong bar magnet is moving towards solenoid-\(2\) from solenoid-\(1\). The direction of induced current in solenoid-\(1\) and that in solenoid-\(2\), respectively, are through the directions:
1. \(BA\) and \(CD\)
2. \(AB\) and \(CD\)
3. \(BA\) and \(DC\)
4. \(AB\) and \(DC\)
1. \(BA\) and \(CD\)
2. \(AB\) and \(CD\)
3. \(BA\) and \(DC\)
4. \(AB\) and \(DC\)
Subtopic: Bar Magnet |
From NCERT
NEET - 2024
Please attempt this question first.
Hints
Please attempt this question first.
An iron bar of length \(\mathrm L\) has magnetic moment \(\mathrm M.\) It is bent at the middle of its length such that the two arms make an angle \(60^\circ\) with each other. The magnetic moment of this new magnet is:
1. \( \mathrm M \over 2\)
2. \( \mathrm {2 M}\)
3. \(\)\(\frac{\mathrm{M}}{\sqrt{3}}\)
4. \(\mathrm M\)
1. \( \mathrm M \over 2\)
2. \( \mathrm {2 M}\)
3. \(\)\(\frac{\mathrm{M}}{\sqrt{3}}\)
4. \(\mathrm M\)
Subtopic: Bar Magnet |
From NCERT
NEET - 2024
Please attempt this question first.
Hints
Please attempt this question first.
The length of a magnetized iron bar is \(L\) and its magnetic moment is \(M.\) When this bar is bent to form a semicircle its magnetic moment is:
| 1. | \(M\) | 2. | \(\dfrac{M\pi}{2}\) |
| 3. | \( \dfrac{M}{2\pi}\) | 4. | \(\dfrac{2M}{\pi}\) |
Subtopic: Bar Magnet |
72%
From NCERT
NEET - 2024
Please attempt this question first.
Hints
Please attempt this question first.
Match List-I with List-II
Choose the correct answer from the options given below:
1. A-I, B-II, C-III, D-IV
2. A-IV,B-III, C-II, D-I
3. A-III, B-II, C-I, D-IV
4. A-II, B-III, C-IV, D-I
| List-I (Material) | List-II (Example) | ||
| A. | Diamagnet | I. | Alnico |
| B. | Paramagnet | II. | Copper |
| C. | Soft ferromagnet | III. | Aluminium |
| D. | Hard ferromagnet | IV. | Gadolinium |
Choose the correct answer from the options given below:
1. A-I, B-II, C-III, D-IV
2. A-IV,B-III, C-II, D-I
3. A-III, B-II, C-I, D-IV
4. A-II, B-III, C-IV, D-I
Subtopic: Magnetic Materials |
52%
From NCERT
NEET - 2024
Please attempt this question first.
Hints
Please attempt this question first.
The best suited curve showing the variations of susceptibility (\(\chi\)) of a paramagnetic material in free space with temperature (\(T\)) is:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Subtopic: Magnetic Materials |
80%
From NCERT
NEET - 2024
Please attempt this question first.
Hints
Please attempt this question first.
Subtopic: Analogy between Electrostatics & Magnetostatics |
82%
From NCERT
NEET - 2023
Please attempt this question first.
Hints
Please attempt this question first.
The variation of susceptibility \((\chi)\) with absolute temperature \((T)\) for a paramagnetic material is represented as:
| 1. |  |
2. |  |
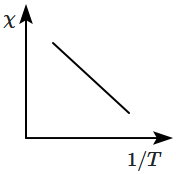| 3. |  |
4. |  |
Subtopic: Curie's Law and Hysteresis (OLD NCERT) |
53%
From NCERT
NEET - 2023
Please attempt this question first.
Hints
Please attempt this question first.
Given below are two statements:
| Assertion (A): | Gauss's law for magnetism states that the net magnetic flux through any closed surface is zero. |
| Reason (R): | The magnetic monopoles do not exist. North and South poles occur in pairs, allowing vanishing net magnetic flux through the surface. |
| 1. | (A) is True but (R) is False. |
| 2. | (A) is False but (R) is True. |
| 3. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 4. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
Subtopic: Analogy between Electrostatics & Magnetostatics |
72%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Select Question Set:
© 2024 GoodEd Technologies Pvt. Ltd.