Select Question Set:
If \(x = 5 \mathrm {sin }\left(\pi t+ {\dfrac {\pi} 3}\right)~\text m\) represents the motion of a particle executing simple harmonic motion, the amplitude and time period of motion, respectively are:
1. \(5~\text m, 2~\text s\)
2. \(5~\text {cm}, 1~\text s\)
3. \(5~\text m, 1~\text s\)
4. \(5~\text {cm}, 2~\text s\)
1. \(5~\text m, 2~\text s\)
2. \(5~\text {cm}, 1~\text s\)
3. \(5~\text m, 1~\text s\)
4. \(5~\text {cm}, 2~\text s\)
Subtopic: Simple Harmonic Motion |
72%
From NCERT
NEET - 2024
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
If the mass of a bob in a simple pendulum is increased to thrice its original mass and its length is made half its original length, then the new time period of oscillation is \( \dfrac{x}{2}\) times its original time period. The value of \(x\) is:
| 1. | \(\sqrt2\) | 2. | \(2\sqrt3\) |
| 3. | \(4\) | 4. | \(\sqrt3\) |
Subtopic: Angular SHM |
68%
From NCERT
NEET - 2024
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
If \(T_1,T_2,T_3,T_4\) and \(T_5\) represent the tension in the string of a simple pendulum when the bob is at the left extreme, right extreme, mean, any intermediate left and any intermediate right positions, respectively. Then, which of the following relations are correct?
Choose the most appropriate answer from the options given below:
| (A) | \(T_1=T_2\) | (B) | \(T_3>T_2\) |
| (C) | \(T_4>T_3\) | (D) | \(T_3=T_4\) |
| (E) | \(T_5>T_2\) | ||
| 1. | (A), (B) and (C) only | 2. | (B), (C) and (D) only |
| 3. | (A), (B) and (E) only | 4. | (C), (D) and (E) only |
Subtopic: Angular SHM |
68%
From NCERT
NEET - 2024
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
The displacement-time \((x\text-t)\) graph of a particle performing simple harmonic motion is shown in the figure. The acceleration of the particle at \(t=2\) s is:


| 1. | \(-\dfrac{\pi^2}{16} ~\text{ms}^{-2}\) | 2. | \(\dfrac{\pi^2}{8}~ \text{ms}^{-2}\) |
| 3. | \(-\dfrac{\pi^2}{8} ~\text{ms}^{-2}\) | 4. | \(\dfrac{\pi^2}{16} ~\text{ms}^{-2}\) |
Subtopic: Simple Harmonic Motion |
66%
From NCERT
NEET - 2023
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
A simple pendulum oscillating in air has a period of \(\sqrt3\) s. If it is completely immersed in non-viscous liquid, having density \(\left(\dfrac14\right)^{\text{th}}\) of the material of the bob, the new period will be:
| 1. | \(2\sqrt3\) s | 2. | \(\dfrac{2}{\sqrt3}\) s |
| 3. | \(2\) s | 4. | \(\dfrac{\sqrt 3}{2}\) s |
Subtopic: Angular SHM |
53%
From NCERT
NEET - 2023
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Two pendulums of length \(121~\text{cm}\) and \(100~\text{cm}\) start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is:
| 1. | \(8\) | 2. | \(11\) |
| 3. | \(9\) | 4. | \(10\) |
Subtopic: Angular SHM |
70%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
During simple harmonic motion of a body, the energy at the extreme position is:
| 1. | both kinetic and potential |
| 2. | is always zero |
| 3. | purely kinetic |
| 4. | purely potential |
Subtopic: Energy of SHM |
80%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Identify the function which represents a non-periodic motion?
| 1. | \(e^{-\omega t}\) | 2. | \(\text{sin}\omega t\) |
| 3. | \(\text{sin}\omega t+\text{cos}\omega t\) | 4. | \(\text{sin}(\omega t+\pi/4)\) |
Subtopic: Types of Motion |
83%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
The restoring force of a spring, with a block attached to the free end of the spring, is represented by:
| 1. |  |
2. |  |
| 3. | 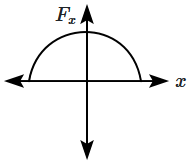 |
4. |  |
Subtopic: Spring mass system |
69%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Match List-I with List-II.
Choose the correct answer from the options given below:
| List-I (\(x \text{-}y\) graphs) |
List-II (Situations) |
||
| (a) |  |
(i) | Total mechanical energy is conserved |
| (b) |  |
(ii) | Bob of a pendulum is oscillating under negligible air friction |
| (c) |  |
(iii) | Restoring force of a spring |
| (d) |  |
(iv) | Bob of a pendulum is oscillating along with air friction |
Choose the correct answer from the options given below:
| (a) | (b) | (c) | (d) | |
| 1. | (iv) | (ii) | (iii) | (i) |
| 2. | (iv) | (iii) | (ii) | (i) |
| 3. | (i) | (iv) | (iii) | (ii) |
| 4. | (iii) | (ii) | (i) | (iv) |
Subtopic: Energy of SHM |
85%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Select Question Set:




