The pressure that has to be applied to the ends of a steel wire of length \(10~\text{cm}\) to keep its length constant when its temperature is raised by \(100^\circ \text{C}\) is:
(Young's modulus of steel is \(2\times 10^{11}~\text{Nm}^{-2}\) and coefficient of thermal expansion is \(1.1 \times 10^{-5}~\text{K}^{-1}\))
1. \( 2.2 \times 10^9 ~\text{Pa} \)
2. \( 2.2 \times 10^7 ~\text{Pa} \)
3. \( 2.2 \times 10^6 ~\text{Pa} \)
4. \( 2.2 \times 10^8 ~\text{Pa} \)

A copper ball of mass \(100~\text{gm}\) is at a temperature \(T.\) It is dropped in a copper calorimeter of mass \(100~\text{gm},\) filled with \(170~\text{gm} \) of water at room temperature. Subsequently, the temperature of the system is found to be \(75^\circ\text{C}. \) \(T\) is given by: (Given: room temperature = \(30^\circ \text{C}, \) specific heat of copper = \(0.1~\text{cal}/ \text{g}~^\circ\text{C}) \)
1. \( 800^{\circ} \text{C} \)
2. \(885^{\circ} \text{C} \)
3. \(1250^{\circ} \text{C} \)
4. \( 825^{\circ} \text{C}\)

An external pressure \(P\) is applied on a cube at \(0^\circ\text{C}\) so that it is equally compressed from all sides. \(K\) is the bulk modulus of the material of the cube and \(\alpha\) is its coefficient of linear expansion. Suppose we want to bring the cube to its original size by heating. The temperature should be raised by:
1. \( \dfrac{{P}}{3 \alpha {K}}\)

2. \( \dfrac{{P}}{\alpha{K}} \)

3. \( \dfrac{3 \alpha}{{PK}} \)

4. \(3 {PK} \alpha\)

Two identical beakers \(A\) and \(B\) contain equal volumes of two different liquids at \(60^\circ\text{C}\) each and left to cool down. Liquid in \(A\) has density of \(8 \times 10^2 ~\text{kg/m}^{3}\) and specific heat of \(2000~\text{Jkg}^{-1} ~\text{K}^{-1}\) while liquid in \(B\) has density of \(10^3 ~\text{kgm}^{-3}\) and specific heat of \(4000~\text{Jkg}^{-1} \text{K}^{-1}\). Which of the following best describes their temperature versus time graph schematically? (assume the emissivity of both the beakers to be the same)

1.		2.
3.		4.

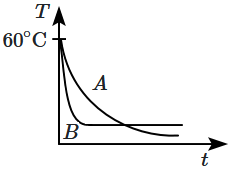A thermally insulated vessel contains \(150~\text{g}\) of water at \(0^\circ\text{C}\). Then the air from the vessel is pumped out adiabatically. A fraction of water turns into ice and the rest evaporates at \(0^\circ\text{C}\) itself. The mass of evaporated water will be closest to: (Latent heat of vaporization of water =\(2.10 \times 10^6 ~\text{Jkg}^{-1}\) and Latent heat of fusion of water = \(3.36 \times 10^5 ~\text{Jkg}^{-1}\))
1. \(130~\text{g}\)
2. \(35~\text{g}\)
3. \(150~\text{g}\)
4. \(20~\text{g}\)

Two materials having coefficients of thermal conductivity '\(3K\)' and '\(K\)' and thickness \(d\) and '\(3d\)' respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are '\(\theta_1\)' and '\(\theta_2\)' respectively, (\(\theta_2>\theta_1\)${}_{}$). The temperature at the interface is:

                 
1. \( \frac{\theta_2+\theta_1}{2} \)
2. \( \frac{\theta_1}{2}+\frac{2 \theta_2}{3} \)
3. \( \frac{\theta_1}{10}+\frac{9 \theta_2}{10} \)
4. \(\frac{\theta_1}{6}+\frac{5 \theta_2}{6}\)