Two identical beakers \(A\) and \(B\) contain equal volumes of two different liquids at \(60^\circ\text{C}\) each and left to cool down. Liquid in \(A\) has density of \(8 \times 10^2 ~\text{kg/m}^{3}\) and specific heat of \(2000~\text{Jkg}^{-1} ~\text{K}^{-1}\) while liquid in \(B\) has density of \(10^3 ~\text{kgm}^{-3}\) and specific heat of \(4000~\text{Jkg}^{-1} \text{K}^{-1}\). Which of the following best describes their temperature versus time graph schematically? (assume the emissivity of both the beakers to be the same)
| 1. |  |
2. |  |
| 3. |  |
4. | 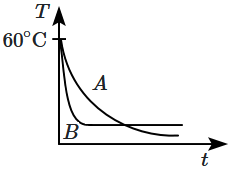 |
Subtopic: Newton's Law of Cooling |
68%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
In an experiment to verify Newton’s Law of Cooling, a graph is plotted between the temperature difference \((\Delta T)\) of water and its surroundings and time, as shown in the figure. The initial temperature of the water is \(80^\circ\text C.\) What is the value of \(t_2 \text{?}\)

1. \(12\)
2. \(14\)
3. \(16\)
4. \(18\)

1. \(12\)
2. \(14\)
3. \(16\)
4. \(18\)
Subtopic: Newton's Law of Cooling |
Level 3: 35%-60%
Please attempt this question first.
Hints
Please attempt this question first.
Read the following statements:
Choose the correct answer from the options given below:
| A. | When small temperature difference between a liquid and its surrounding is doubled the rate of loss of heat of the liquid becomes twice. |
| B. | Two bodies P and Q having equal surface areas are maintained at temperature 10ºC and 20 ºC. The thermal radiation emitted in a given time by P and Q are in the ratio 1 : 1.15 |
| C. | A car engine working between 100 K and 400 K has an efficiency of 75% |
| D. | When small temperature difference between a liquid and its surrounding is quadrupled, the rate of loss of heat of the liquid becomes twice. |
Choose the correct answer from the options given below:
| 1. | A, B, C only |
| 2. | A, B only |
| 3. | A, C only |
| 4. | B, C, D only |
Subtopic: Newton's Law of Cooling |
52%
Level 3: 35%-60%
JEE
Please attempt this question first.
Hints
Please attempt this question first.
The temperature of hot soup in a bowl goes \(98^{\circ}\) C to \(86^{\circ}\) C in \(2\) min. The temperature of the surrounding is \(22^{\circ}\) C. What is the time taken for the temperature of the soup to go from \(75^{\circ}\) C to \(69^{\circ}\) C?
(Assume Newton’s law of cooling is valid)
1. \(1\) min
2. \(1.4\) min
3. \(2\) min
4. \(3.2\) min
(Assume Newton’s law of cooling is valid)
1. \(1\) min
2. \(1.4\) min
3. \(2\) min
4. \(3.2\) min
Subtopic: Newton's Law of Cooling |
77%
Level 2: 60%+
Please attempt this question first.
Hints
Please attempt this question first.
The temperature of body drops from \(60^\circ \mathrm{C}\) to \(40^\circ \mathrm{C}\) in \(7\) min. The surrounding temperature is \(10^\circ \mathrm{C}.\) The temperature of body drops from \(40^\circ \mathrm{C}\) to \(\mathrm{T}^\circ \mathrm{C}\) in \(7\) min. The value of \(\mathrm{T}\) is:
1. \(16^\circ \mathrm{C}\)
2. \(20^\circ \mathrm{C}\)
3. \(28^\circ \mathrm{C}\)
4. \(36^\circ \mathrm{C}\)
1. \(16^\circ \mathrm{C}\)
2. \(20^\circ \mathrm{C}\)
3. \(28^\circ \mathrm{C}\)
4. \(36^\circ \mathrm{C}\)
Subtopic: Newton's Law of Cooling |
71%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
An object cools down from \(80^\circ \text{C}\) to \(60^\circ \text{C}\) in \(5\) min in a surrounding of temperature \(20^\circ \text{C}.\) The time taken to cool from \(60^\circ \text{C}\) to \(40^\circ \text{C}\) will be:
(Assume Newton's law of cooling to be valid.)
(Assume Newton's law of cooling to be valid.)
| 1. | \({ 25 \over 3} ~\text {min}\) | 2. | \(5 ~\text {min}\) |
| 3. | \({ 25 \over 4} ~\text {min}\) | 4. | \(9~ \text {min}\) |
Subtopic: Newton's Law of Cooling |
79%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.




