The radius of gyration of a uniform solid sphere about a tangent is:
1.
2.
3.
4.
Three identical spheres, each of mass \(M\), are placed at the corners of a right-angle triangle with mutually perpendicular sides equal to \(2~\text{m}\) (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of the centre of mass.
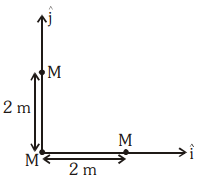
| 1. | \(2( \hat{i}+ \hat{j})\) | 2. | \(( \hat{i}+ \hat{j})\) |
| 3. | \({2 \over 3}( \hat{i}+ \hat{j})\) | 4. | \({4 \over 3}( \hat{i}+ \hat{j})\) |
The coordinates of the centre of mass of a uniform plate of shape as shown in the figure are:

| 1. | \(\frac{L}{2}, \frac{L}{2} \) | 2. | \(\frac{5 L}{12}, \frac{5 L}{12} \) |
| 3. | \(\frac{5L}{3}, \frac{2L}{3}\) | 4. | \(\frac{3 L}{4}, \frac{L}{2}\) |
A rigid body rotates with an angular momentum of \(L.\) If its kinetic energy is halved, the angular momentum becomes:
1. \(L\)
2. \(L/2\)
3. \(2L\)
4. \(L/\)
1. \(0.25~\text{rad/s}^2\)
2. \(25~\text{rad/s}^2\)
3. \(5~\text{m/s}^2\)
4. \(25~\text{m/s}^2\)
A particle is moving with a constant velocity along a line parallel to the positive x-axis. The magnitude of its angular momentum with respect to the origin is:
| 1. | zero |
| 2. | increasing with \(x\) |
| 3. | decreasing with \(x\) |
| 4. | remaining constant |
The center of mass of a system of particles does not depend upon:
| 1. | position of particles |
| 2. | relative distance between particles |
| 3. | masses of particles |
| 4. | force acting on the particle |
A uniform square plate \(ABCD\) has a mass of \(10\) kg.
If two point masses of \(5\) kg each are placed at the corners \(C\) and \(D\) as shown in the adjoining figure, then the centre of mass shifts to the mid-point of:

1. \(OH\)
2. \(DH\)
3. \(OG\)
4. \(OF\)
At \(t=0,\) the positions of the two blocks are shown. There is no external force acting on the system. Find the coordinates of the centre of mass of the system (in SI units) at \(t=3\) seconds.

| 1. | \((1,0)\) | 2. | \((3,0)\) |
| 3. | \((4.5,0)\) | 4. | \((2.25,0)\) |
The mass per unit length of a non-uniform rod of length \(L\) is given by \(\mu =λx^{2}\) where \(\lambda\) is a constant and \(x\) is the distance from one end of the rod. The distance between the centre of mass of the rod and this end is:
| 1. | \(\frac{L}{2}\) | 2. | \(\frac{L}{4}\) |
| 3. | \(\frac{3L}{4}\) | 4. | \(\frac{L}{3}\) |






