+91-8527521718
Signup | Login
  • 1(current)
Q. No.
A block of mass \(m\) slides down the smooth inclined surface of a wedge of mass \(M;\) which is itself on a smooth horizontal surface. The centre-of-mass of the system:
                  
1. is stationary
2. accelerates to the left
3. accelerates to the right
4. accelerates downward
Subtopic:  Center of Mass |
Level 4: Below 35%
Hints
A uniform chain \(ABC\) is at rest with half of it hanging off the edge of a rough horizontal table. If the total length of the chain is \(2~\text m,\) the centre-of-mass of the chain is located:
                 
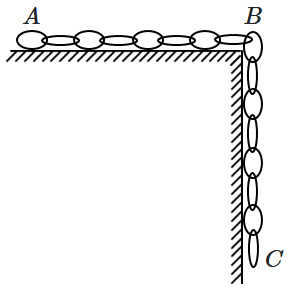
1. \(0.25~\text{m}\) below the table 
2. \(0.5~\text{m}\) below the table
3. \(0.33~\text{m}\) below the table
4. \(0.4~\text{m}\) below the table
Subtopic:  Center of Mass |
Level 3: 35%-60%
Hints
A block of mass \(m\) is placed atop another block of mass \(M,\) and the combination is at rest on a smooth horizontal table. A force \(F_1\) is applied to \(m\) and another force \(F_2\) is applied to \(M,\) the two acting horizontally and in opposite directions. Consider the following statements about the acceleration \((a_{cm})\) of the centre of mass of the system). 
(take right as positive)
                          
(A) \(a_{cm}=\dfrac{F_1-F_2}{m+M},\) if there is no friction acting between \(m\) and \(M\)
(B) \(a_{cm}=\dfrac{F_1-F_2}{m+M},\) if there is static friction between \(m\) and \(M\)
(C) \(a_{cm}=\dfrac{F_1-F_2}{m+M},\) in all situations
Choose the most appropriate option from the given ones:
1. only (A) is True.
2. only (B) is True.
3. (C) is True.
4. (A) and (B) are True but (C) is False.
Subtopic:  Center of Mass |
Level 3: 35%-60%
Hints
advertisementadvertisement
A thin spherical metallic vessel of radius \(R\) contains water, the mass of water being equal to the mass of the vessel that contains it. A hole is made in the bottom so that the water begins to flow out. When the vessel is half-empty the centre-of-mass is at a distance \(d\) from the centre of the vessel:
1. \(d=\dfrac{3 R}{16}\) 2. \(d=\dfrac{R}{2}\)
3. \(d=\dfrac{R}{4}\) 4. \(d=\dfrac{R}{8}\)
Subtopic:  Center of Mass |
Level 3: 35%-60%
Hints
A thin uniform hemispherical shell (radius: \(R,\) center: \(O\)) is cut into two symmetric quarter spheres by means of a vertical plane, as shown. The centre-of-mass of a quarter sphere is at a distance \(d\) from \(O\). Then \(d\)=    
1. \(\dfrac R2\) 2. \(\dfrac R{\sqrt2}\)
3. \(\dfrac R{4}\) 4. \(\dfrac R{2\sqrt2}\)
Subtopic:  Center of Mass |
Level 3: 35%-60%
Hints
The centre-of-mass of a uniform solid cone is located at a distance of \(\dfrac{3}{4} H\) from the vertex of the cone, where \(H\) is its height. The centre-of-mass of a regular solid tetrahedron of height \(H\) is located at a distance of:
1. \(\dfrac{1}{2} H\) from its vertex
2. \(\dfrac{2}{3}H\) from its vertex
3. \(\dfrac{3}{4}H\) from its vertex
4. \(\dfrac{3}{8}H\) from its vertex
Subtopic:  Center of Mass |
 56%
Level 3: 35%-60%
Hints
advertisementadvertisement
A block of mass \(m\) slides down the smooth inclined surface of a wedge of mass \(M\) starting from rest. The wedge is at rest on the horizontal surface beneath it, due to friction. The acceleration of the center of mass of the system of the block and the wedge is:
1. \(\dfrac{mg~\text{sin}\theta}{m+M}\) 2. \(\dfrac{mg~\text{cos}\theta}{m+M}\)
3. \(g~\text{sin}\theta\) 4. zero
Subtopic:  Center of Mass |
 55%
Level 3: 35%-60%
Hints
The centre-of-mass of a uniform solid hemisphere of radius \(R\) is located at a distance of \(\dfrac{3R}{8}\) from its centre \(O.\) If the hemisphere is now cut symmetrically into two identical parts by a single plane, the centre-of-mass of one of the parts is located at a distance from \(O\) of:
1. \(\dfrac{3R}{8}\)

2. \(\dfrac{3R}{4}\)

3. \(\dfrac{3R}{8}\sqrt2\)

4. \(\dfrac{3R}{5}\sqrt2\)
Subtopic:  Center of Mass |
 57%
Level 3: 35%-60%
Hints
Given below are two statements: 
Statement I: The centre-of-mass of a system of particles lying on a straight line must lie between the two extreme particles.
Statement II: The centre-of-mass of a system of bodies moving with different velocities, cannot be moving with constant velocity.
 
1. Statement I is incorrect and Statement II is correct.
2. Both Statement I and Statement II are correct.
3. Both Statement I and Statement II are incorrect.
4. Statement I is correct and Statement II is incorrect.
Subtopic:  Center of Mass |
 58%
Level 3: 35%-60%
Hints
advertisementadvertisement
A thin uniform hemispherical shell (radius: \(R\)) is placed upside down: with its open end down. It is cut into two parts by a horizontal plane, so that the masses of the two parts are equal. The centre-of-mass of the lower part is located at a distance of:
             

1. \(\dfrac R3\) from \(O\)

2. \(\dfrac R4\) from \(O\)

3. \(\dfrac R6\) from \(O\)

4. \(\dfrac R8\) from \(O\)
Subtopic:  Center of Mass |
 60%
Level 2: 60%+
Hints
  • 1(current)
Q. No.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions

© 2025 GoodEd Technologies Pvt. Ltd.