Consider a spherical shell of radius \(R\) at temperature \(T\). The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume \({u}=\frac{U}{V}\propto T^4\) and \(P=\frac{1}{3}\left(\frac{U}{V}\right )\). If the shell now undergoes an adiabatic expansion the relation between \(T\) and \(R\) is:
1. \({T} \propto {e}^{-{R}} \)
2. \({T} \propto {e}^{-3 {R}} \)
3. \({T} \propto \frac{1}{{R}} \)
4. \({T} \propto \frac{1}{{R}^3}\)
Consider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increases as \(V^q\), where \(V\) is the volume of the gas. The value of \(q\) is: \((\gamma =\frac{C_P}{C_V})\)
1. \( \frac{3 \gamma+5}{6} \)
2. \(\frac{3 \gamma-5}{6} \)
3. \(\frac{\gamma+1}{2} \)
4. \(\frac{\gamma-1}{2}\)
'\(n\)' moles of an ideal gas undergo a process \(A\rightarrow B\) as shown in the figure. The maximum temperature of the gas during the process will be:
1. \( \frac{9 P_0 V_0}{4 n R} \)
2. \(\frac{3 P_0 V_0}{2 n R} \)
3. \(\frac{9 P_0 V_0}{2 n R} \)
4. \(\frac{9 P_0 V_0}{n R}\)

| 1. |  |
3. |  |
| 2. |  |
4. |  |
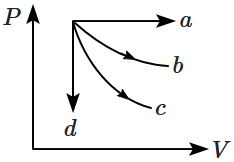
The given diagram shows four processes i.e., isochoric, isobaric, isothermal and adiabatic. The correct assignment of the processes, in the same order, is given by:
1. \(d,~a,~b,~c\)
2. \(a,~d,~c,~b\)
3. \(a,~d,~b,~c\)
4. \(d,~a,~c,~b\)
An engine takes in \(5\) moles of air at \(20^\circ\) C and \(1\) atm, and compresses it adiabaticaly to \(1/10\) th of the original volume. Assuming air to be a diatomic ideal gas made up of rigid molecules, the change in its internal energy during this process comes out to be:
1. \(46~ \text{J}\)
2. \(46~\text{kJ}\)
3. \(23~\text{J}\)
4. \(23~\text{kJ}\)
A balloon filled with helium (\(32^\circ \mathrm{C}\) and \(1.7\) atm) bursts. Immediately afterwards the expansion of helium can be considered as:
| 1. | irreversible adiabatic |
| 2. | reversible adiabatic |
| 3. | irreversible isothermal |
| 4. | reversible isothermal |
A closed vessel contains \(0.1\) mole of a monatomic ideal gas at \(200\) K. If \(0.05\) mole of the same gas at \(400\) K is added to it, the final equilibrium temperature (in K) of the gas in the vessel will be closed to:
1. \(133\)
2. \(57\)
3. \(266\)
4. \(504\)
Match the thermodynamic processes taking place in a system with the correct conditions. In the table: \(\Delta Q\) is the heat supplied, \(\Delta W\) is the work done and \(\Delta U\) is change in internal energy of the system.
| Process | Condition | ||
| (I) | Adiabatic | (A) | \(\Delta W=0\) |
| (II) | Isothermal | (B) | \(\Delta Q=0\) |
| (III) | Isochoric | (C) | \(\Delta U\neq0,\Delta W\neq0,\Delta Q\neq0\) |
| (IV) | Isobaric | (D) | \(\Delta U=0\) |
| 1. | (I) – (B), (II) – (A), (III) – (D), (IV) – (C) |
| 2. | (I) – (A), (II) – (A), (III) – (B), (IV) – (C) |
| 3. | (I) – (A), (II) – (B), (III) – (D), (IV) – (D) |
| 4. | (I) – (B), (II) – (D), (III) – (A), (IV) – (C) |
The change in the magnitude of the volume of an ideal gas when a small additional pressure \(\Delta P\) is applied at constant temperature, is the same as the change when the temperature is reduced by a small quantity \(\Delta T\) at constant pressure. The initial temperature and pressure of the gas were \(300~\text{K}\) and \(2~\text{atm}\). respectively. If \(|\Delta T|=C|\Delta P|\) then the value of \(C\) in ( K/atm) is:
1. \(50\)
2. \(100\)
3. \(150\)
4. \(200\)