If \(a,b,c,\) and \(d\) are inputs to a logic gate and \(x\) is its output, then based on the timing diagram shown below, what type of gate is this?
1. NOT
2. AND
3. OR
4. NAND
The logic gate equivalent to the given logic circuit is:
1. AND
2. OR
3. NOR
4. NAND
The truth table for the circuit given in the fig. is:
| 1. | \(A\) | \(B\) | \(Y\) | 2. | \(A\) | \(B\) | \(Y\) |
| 0 | 0 | 1 | 0 | 0 | 1 | ||
| 0 | 1 | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 1 | 1 | 0 | 0 | ||
| 1 | 1 | 1 | 1 | 1 | 0 | ||
| 3. | \(A\) | \(B\) | \(Y\) | 4. | \(A\) | \(B\) | \(Y\) |
| 0 | 0 | 0 | 0 | 0 | 1 | ||
| 0 | 1 | 0 | 0 | 1 | 0 | ||
| 1 | 0 | 1 | 1 | 0 | 0 | ||
| 1 | 1 | 1 | 1 | 1 | 0 | ||
In the digital logic circuit shown, what is the sequence of output values at terminal \(Z\) corresponding to the input combinations \((A,B)=(1,0),(0,0),(1,1)\) and \((0,1)\text{?}\)
| 1. | \(1,0,1,1\) |
| 2. | \(0,1,0,0\) |
| 3. | \(0,0,1,0\) |
| 4. | \(1,1,0,1\) |
Identify the operation performed by the circuit given below:
1. \(\text{OR}\)
2. \(\text{NOT}\)
3. \(\text{NAND}\)
4. \(\text{AND}\)
The logic circuit shown above is equivalent to :
| 1. | 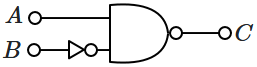 |
| 2. |  |
| 3. |  |
| 4. |  |
The truth table for the following logic circuit is :
| 1. | A | B | Y | 2. | A | B | Y | |
| 0 | 0 | 0 | 0 | 0 | 1 | |||
| 0 | 1 | 1 | 0 | 1 | 0 | |||
| 1 | 0 | 1 | 1 | 0 | 0 | |||
| 1 | 1 | 0 | 1 | 1 | 1 | |||
| 3. | A | B | Y | 4. | A | B | Y | |
| 0 | 0 | 1 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 0 | 1 | 1 | |||
| 1 | 0 | 1 | 1 | 0 | 0 | |||
| 1 | 1 | 0 | 1 | 1 | 1 | |||
Draw the output signal \(Y\) in the given combination of gates :
| 1. |  |
| 2. |  |
| 3. |  |
| 4. |  |

1. AND gate
2. OR gate
3. NOR gate
4. NAND gate

| 1. |  |
| 2. |  |
| 3. |  |
| 4. | none of these |














