Water from a tap emerges vertically downwards with an initial speed of \(1.0~\text{m/s}\). The cross-sectional area of the tap is \(10^{-4}~\text{m}^2\). Assume that the pressure is constant throughout the stream of water and that the flow is streamlined. The cross-sectional area of the stream, \(0.15~\text{m}\) below the tap would be: (take \(g=10~\text{m/s}^2\))
1. \(5\times10^{-4}~\text{m}^2\)
2. \(2\times10^{-5}~\text{m}^2\)
3. \(5\times10^{-5}~\text{m}^2\)
4. \(1\times10^{-5}~\text{m}^2\)
A fluid is flowing through a horizontal pipe of varying cross-sections, with speed \(v\) ms-1 at a point where the pressure is \(P\) pascal. At another point where pressure is \(\dfrac{P}{2}\) pascal, its speed is \(V\) ms-1. If the density of the fluid is \(\rho\) kg-m-3 and the flow is streamlined, then \(V\) is equal to:
| 1. | \(\sqrt{\dfrac{P}{2\rho }+v^{2}}\) | 2. | \(\sqrt{\dfrac{P}{\rho }+v^{2}} \) |
| 3. | \(\sqrt{\dfrac{2P}{\rho }+v^{2}}\) | 4. | \(\sqrt{\dfrac{P}{\rho }+v^{}}\) |
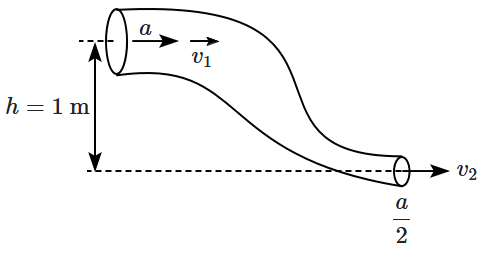
1. \(124\)
2. \(236\)
3. \(363\)
4. \(432\)
1. \(1~\text{ms}^{-1}\)
2. \(2~\text{ms}^{-1}\)
3. \(3~\text{ms}^{-1}\)
4. \(4~\text{ms}^{-1}\)
1. \(20\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
2. \(30\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
3. \(28\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
4. \(24\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
(assume incompressible fluid, density of water = \(1000~\text{kg/m}^3\) )

1. \(175\times 10^4~ \text{Pa}\)
2. \(175\times 10^3~ \text{Pa}\)
3. \(250\times 10^4~ \text{Pa}\)
4. \(250\times 10^3~ \text{Pa}\)

1. \(22\)
2. \(33\)
3. \(11\)
4. \(55\)
1. \(P+\rho g h+\frac{1}{2} \rho v^2=\text { constant }\)
2. \(\mathrm{P}+\rho \mathrm{gh}+\rho \mathrm{v}^2=\mathrm{constant}\)
3. \(P+\mathrm{mgh}+\frac{1}{2} \mathrm{mv}^2=\text { constant }\)
4. \(\mathrm{P}+\frac{1}{2} \rho g h+\frac{1}{2} \rho \mathrm{v}^2=\text { constant }\)




