An engine operates by taking n moles of an ideal gas through the cycle \(ABCDA\) shown in the figure. The thermal efficiency of the engine is:
(Take \({C}_v=1.5{R},\) where \({R}\) is gas constant)

1. \(0.32\)
2. \(0.15\)
3. \(0.24\)
4. \(0.08\)
(Take \({C}_v=1.5{R},\) where \({R}\) is gas constant)

1. \(0.32\)
2. \(0.15\)
3. \(0.24\)
4. \(0.08\)
Subtopic: Carnot Engine |
63%
Level 2: 60%+
Please attempt this question first.
Hints
Please attempt this question first.
A carnot's engine works as a refrigerator between \(250~\text{K}\) and \(300~\text{K}.\) It receives \(500~ \text{cal}\) heat from the reservoir at a lower temperature. The amount of work done in each cycle to operate the refrigerator is:
1. \(772 ~\text{J}\)
2. \(420 ~\text{J}\)
3. \(2100 ~\text{J}\)
4. \(2520 ~\text{J}\)
1. \(772 ~\text{J}\)
2. \(420 ~\text{J}\)
3. \(2100 ~\text{J}\)
4. \(2520 ~\text{J}\)
Subtopic: Carnot Engine |
71%
Level 2: 60%+
Please attempt this question first.
Hints
Please attempt this question first.
A Carnot engine whose heat sinks at \(27^\circ \text{C},\) has an efficiency of \(25\text{%}.\) By how many degrees should the temperature of the source be changed to increase the efficiency by \(100\text{%}\) of the original efficiency?
1. Increase by \(18^\circ \text{C}\)
2. Increase by \(200^\circ \text{C}\)
3. Increase by \(120^\circ \text{C}\)
4. Increase by \(73^\circ \text{C}\)
1. Increase by \(18^\circ \text{C}\)
2. Increase by \(200^\circ \text{C}\)
3. Increase by \(120^\circ \text{C}\)
4. Increase by \(73^\circ \text{C}\)
Subtopic: Carnot Engine |
70%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
A Carnot engine takes \(5000~\text{kcal}\) of heat from a reservoir at \(727^\circ \text{C}\) and gives heat to a sink at \(127^\circ \text{C}.\) The work done by the engine is:
1. \(3 \times 10^6 ~\text J\)
2. zero
3. \(12.6 \times 10^6 \)
4. \(8.4 \times 10^6 \)
1. \(3 \times 10^6 ~\text J\)
2. zero
3. \(12.6 \times 10^6 \)
4. \(8.4 \times 10^6 \)
Subtopic: Carnot Engine |
61%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
The efficiency of a Carnot's engine, working between the steam point and ice point, will be:
| 1. | \(26.81\text{%}\) | 2. | \(37.81\text{%}\) |
| 3. | \(47.81\text{%}\) | 4. | \(57.81\text{%}\) |
Subtopic: Carnot Engine |
77%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
In a Carnot engine, the temperature of the reservoir is \(527^\circ \text{C}\) and that of the sink is \(200\) K. If the work done by the engine when it transfers heat from the reservoir to sink is \(12000\) kJ, the quantity of heat absorbed by the engine from the reservoir is:
1. \(12\times10^6\) J
2. \(14\times10^6\) J
3. \(16\times10^6\) J
4. \(18\times10^6\) J
1. \(12\times10^6\) J
2. \(14\times10^6\) J
3. \(16\times10^6\) J
4. \(18\times10^6\) J
Subtopic: Carnot Engine |
82%
Level 1: 80%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
\(300\) calories of heat is given to a heat engine and it rejects \(225\) calories of heat. If source temperature is \(227^\circ \text{C}\), then the temperature of sink will be:
1. \(102^\circ \text{C}\)
2. \(90^\circ \text{C}\)
3. \(110^\circ \text{C}\)
4. \(120^\circ \text{C}\)
1. \(102^\circ \text{C}\)
2. \(90^\circ \text{C}\)
3. \(110^\circ \text{C}\)
4. \(120^\circ \text{C}\)
Subtopic: Carnot Engine |
83%
Level 1: 80%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
In the first case, a Carnot engine operates between temperatures of \(300~\text{K}\) and \(100~\text{K}.\) In the second case, as shown in the figure, two heat engines are connected in series (i.e., the output of the first engine becomes the input for the second engine).
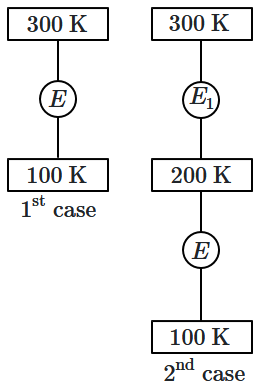
What is the overall efficiency of the combined engine system in the second case?
| 1. | Same as the first case. |
| 2. | Always greater than the first case. |
| 3. | Always less than the first case. |
| 4. | May increase or decrease with respect to the first case. |
Subtopic: Carnot Engine |
Level 3: 35%-60%
Please attempt this question first.
Hints
Please attempt this question first.
A Carnot engine has an efficiency of \(50\%\). If the temperature of sink is reduced by \(40^{\circ}\text{C}\), its efficiency increases by \(30\%\). The temperature of the source will be:
1. \(166.7\) K
2. \(255.1\) K
3. \(266.7\) K
4. \(367.7\) K
1. \(166.7\) K
2. \(255.1\) K
3. \(266.7\) K
4. \(367.7\) K
Subtopic: Carnot Engine |
59%
Level 3: 35%-60%
Please attempt this question first.
Hints
Please attempt this question first.
A Carnot engine working between a source and a sink at \(200~\text K\) has an efficiency of \(50\%.\) Another Carnot engine working between the same source and another sink with an unknown temperature \(T\) has an efficiency of \(75\text{%}.\) The value of \(T\) is equal to:
1. \(400 ~\text K\)
2. \(300 ~\text K\)
3. \(200 ~\text K\)
4. \(100 ~\text K\)
1. \(400 ~\text K\)
2. \(300 ~\text K\)
3. \(200 ~\text K\)
4. \(100 ~\text K\)
Subtopic: Carnot Engine |
74%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.






