Two bodies of mass, \(4~\text{kg}\) and \(6~\text{kg}\), are tied to the ends of a massless string. The string passes over a pulley, which is frictionless (see figure). The acceleration of the system in terms of acceleration due to gravity (\(g\)) is:

1.
\(\dfrac{g}{2}\)
2.
\(\dfrac{g}{5}\)
3.
\(\dfrac{g}{10}\)
4.
\(g\)

A point mass \(m\) is moved in a vertical circle of radius \(r\) with the help of a string. The velocity of the mass is \(\sqrt{7gr} \) at the lowest point. The tension in the string at the lowest point is:
| 1. | \(6 \text{mg}\) | 2. | \(7 \text{mg}\) |
| 3. | \(8 \text{mg}\) | 4. | \( \text{mg}\) |
Calculate the acceleration of the block and trolly system shown in the figure. The coefficient of kinetic friction between the trolly and the surface is \(0.05.\)
( \(g=10~\text{m/s}^2,\) the mass of the string is negligible and no other friction exists)
| 1. | \( 1.25~\text{m/s}^2\) | 2. | \( 1.50~\text{m/s}^2\) |
| 3. | \(1.66~\text{m/s}^2\) | 4. | \( 1.00~\text{m/s}^2\) |
A body of mass \(m\) is kept on a rough horizontal surface (coefficient of friction = \(\mu).\) A horizontal force is applied to the body, but it does not move. The resultant of normal reaction and the frictional force acting on the object is given by \(\vec {F}\) where:
1. \(|{\vec {F}}| = mg+\mu mg\)
2. \(|\vec {F}| =\mu mg\)
3. \(|\vec {F}| \le mg\sqrt{1+\mu^2}\)
4. \(|\vec{F}| = mg\)
A truck is stationary and has a bob suspended by a light string in a frame attached to the truck. The truck suddenly moves to the right with an acceleration of \(a.\) In the frame of the truck, the pendulum will tilt:
| 1. | to the left and the angle of inclination of the pendulum with the vertical is \(\text{sin}^{-1} \left( \dfrac{a}{g} \right )\) |
| 2. | to the left and the angle of inclination of the pendulum with the vertical is \(\text{cos}^{-1} \left ( \dfrac{a}{g} \right )\) |
| 3. | to the left and the angle of inclination of the pendulum with the vertical is \(\text{tan}^{-1} \left ( \dfrac{a}{g} \right )\) |
| 4. | to the left and the angle of inclination of the pendulum with the vertical is \(\text{tan}^{-1} \left ( \dfrac{g}{a} \right )\) |
A car of mass \(m\) is moving on a level circular track of radius \(R\). If \(\mu_s\) represents the static friction between the road and tyres of the car, the maximum speed of the car in circular motion is given by:
| 1. | \(\sqrt{\dfrac{Rg}{\mu_s} }\) | 2. | \(\sqrt{\dfrac{mRg}{\mu_s}}\) |
| 3. | \(\sqrt{\mu_s Rg}\) | 4. | \(\sqrt{\mu_s m Rg}\) |
A conveyor belt is moving at a constant speed of \(2\) m/s. A box is gently dropped on it. The coefficient of friction between them is \(\mu = 0.5\). The distance that the box will move relative to the belt before coming to rest on it, taking \(g = 10\) ms–2 is:
| 1. | \(0.4\) m | 2. | \(1.2\) m |
| 3. | \(0.6\) m | 4. | zero |
A small mass attached to a string rotates on a frictionless table top as shown. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will:
1. decrease by a factor of 2
2. remain constant
3. increase by a factor of 2
4. increase by a factor of 4
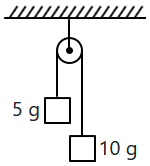
Two masses as shown are suspended from a massless pulley. What would be the acceleration of the system when masses are left free?
1. \(2g/3\)
2. \(g/3\)
3. \(g/9\)
4. \(g/7\)
(where \(g\) is the acceleration due to gravity.)
A body of mass 3 kg hits a wall at an angle of 60º & returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
1. 150 N
2. 50 N
3. 100 N
4. 75 N