A body is projected vertically upward and then allowed to fall back down under gravity. Which of the following velocity–time \((v \text-t) \) graphs correctly represents its motion throughout the ascent and descent?
| 1. |  |
2. |  |
| 3. |  |
4. |  |

1. \(112.5\text{ m and}~ 22.5~ \text{s} \)
2. \(337.5\text{ m and}~ 25~ \text{s} \)
3. \(225.5\text{ m and}~ 10~ \text{s} \)
4. \(112.5\text{ m and}~ 15~ \text{s} \)
A ball is thrown vertically up (taken as \(+z\)-axis) from the ground. The correct momentum\(\text-\)height (\(p\text{-}h\)) diagram is:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
A tennis ball is released from a height \(h\) and after freely falling on a wooden floor it rebounds and reaches height \(\frac{h}{2}\). The velocity versus height of the ball during its motion may be represented graphically by:
(graph are drawn schematically and on not to scale)
| 1. |  |
2. |  |
| 3. | 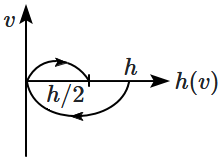 |
4. |  |
The velocity (\(v\)) and time (\(t\)) graph of a body in a straight-line motion is shown in the figure. The point \(S\) occurs at \(4.333\) seconds. The total distance covered by the body in \(6\) s is:
1. \(12\) \(\text{m}\)
2. \(\dfrac{49}{12}\) \(\text{m}\)
3. \(11\) \(\text{m}\)
4. \(\dfrac{37}{3}\) \(\text{m} \)
If the velocity-time graph has the shape \(AMB,\) what would be the shape of the corresponding acceleration-time graph?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
| 1. | 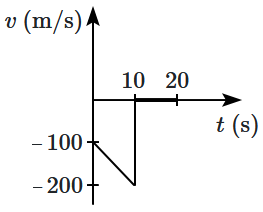 |
2. |  |
| 3. | 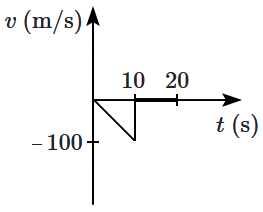 |
4. | 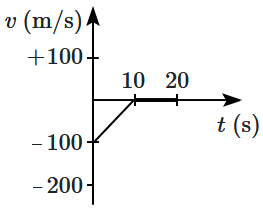 |

Choose the corresponding \((v\text-t)\) graph.
| 1. |  |
2. |  |
| 3. |  |
4. | 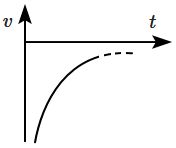 |

| a. | \(\mathrm{A}\) is faster than \(\mathrm{B}\) |
| b. | \(\mathrm{B}\) is faster than \(\mathrm{A}\) |
| c. | \(\mathrm{B}\) lives further away than \(\mathrm{A}\) |
| d. | \(\mathrm{A}\) live further away than \(\mathrm{B}\) |
Choose the correct entries:
| 1. | (a), (d) |
| 2. | (b), (c) |
| 3. | (b), (d) |
| 4. | (a), (c) |
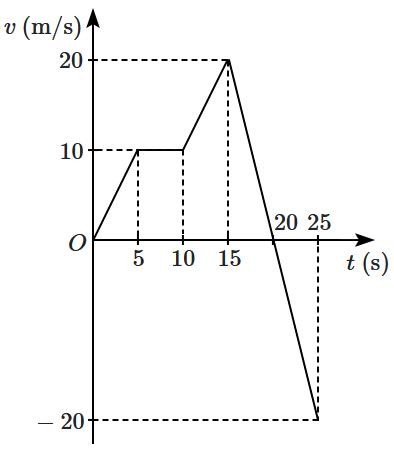
1. 150 m and 250 m
2. 250 m and 250 m
3. 150 m and 150 m
4. 50 m and 150 m








