| 1. | The left arm is shorter than the right arm. |
| 2. | Both arms are of equal length. |
| 3. | Every object measured with this balance appears lighter than its actual weight. |
| 4. | The left arm is longer than the right arm. |
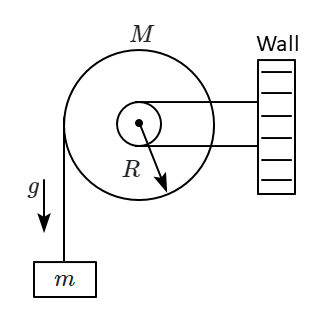
1. \(\frac{2{Mg}}{2{m + M}}\)`
2. \(\frac{2{mg}}{2{m + M}}\)
3. \(\frac{2{Mg}}{2{M + m}}\)
4. \(\frac{2{mg}}{2{M + m}}\)
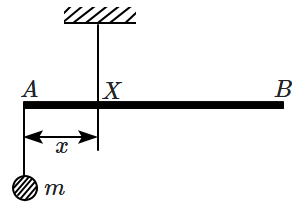
1. \(m,x^2 \)
2. \(m,\dfrac{1}{x^2}\)
3. \(m,\dfrac{1}{x} \)
4. \(m,x \)

1. \(\tan \theta = 4 \)
2. \(\tan \theta = \dfrac{1}{4} \)
3. \(\tan \theta = \dfrac{1}{2} \)
4. \(\tan\theta = 2 \)
A rectangular solid box of length \(0.3~\text{m}\) is held horizontally, with one of its sides on the edge of a platform of height \(5~\text{m}\). When released, it slips off the table in a very short time \(\tau=0.01~\text{s}\), remaining essentially horizontal. The angle by which it would rotate when it hits the ground will be (in radians) close to:
1. \(0.5\)
2. \(0.02\)
3. \(0.28\)
4. \(0.3\)
A particle of mass \(m\) is moving along a trajectory given by:
\(\begin{aligned} & x=x_0+a \cos \omega_1 t \\ & y=y_0+b \sin \omega_2 t \end{aligned}\)
The torque, acting on the particle about the origin, at \(t=0\) is:
1. \( -m\left(x_0 b \omega_2^2-y_0 a \omega_1^2\right) \hat{k} \)
2. \( \text { zero } \)
3. \( +m y_0 a \omega_1^2 \hat{k} \)
4. \( m\left(-x_0 b+y_0 a\right) \omega_1^2 \hat{k}\)
A metal coin of mass \(5~\text{g}\) and radius \(1~\text{cm}\) is fixed to a thin stick \(AB\) of negligible mass as shown in the figure. The system is initially at rest. The constant torque, that will make the system rotate about \(AB\) at \(25\) rotations per second in \(5~\text{s}\), is close to:
1. \( 7.9 \times 10^{-6} ~\text{Nm} \)
2. \(4.0 \times 10^{-6} ~\text{Nm} \)
3. \( 2.0 \times 10^{-5} ~\text{Nm} \)
4. \( 1.6 \times 10^{-5} ~\text{Nm}\)
In the figure, there's a rigid and uniform rod \(AB,\) one meter long, held horizontally by two strings tied to its ends and attached to the ceiling. The rod has a mass of \(m\) and another weight of the mass \(2m\) is hung at a distance of \(75\) cm from \(A.\) The tension in the string at the point \(A\) is:
1. \(2mg\)
2. \(0.5mg\)
3. \(0.75 mg\)
4. \(mg\)
A uniform cylinder of mass \(M\) and radius \(R\) is to be pulled over a step of height \(a\) (\(a<R\)) by applying a force \(F\) at its centre '\(O\)' perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). The minimum value of \(F\) required is :
1. \( M g \sqrt{1-\frac{a^2}{R^2}} \)
2. \( M g \sqrt{\left(\frac{R}{R-a}\right)^2-1} \)
3. \(M g \frac{a}{R} \)
4. \( M g \sqrt{1-\left(\frac{R-a}{R}\right)^2} \)
A force \(\vec{F}=\hat{i}+2\hat{j}+3\hat{k}~\text{N}\) acts at a point \(\hat{4i}+3\hat{j}-\hat{k}~\text{m}\). Let the magnitude of the torque about the point \(\hat{i}+2\hat{j}+\hat{k}~\text{m}\) be \(\sqrt{x}~\text{N-m}\). The value of \(x\) is:
1. \(145\)
2. \(195\)
3. \(245\)
4. \(295\)










